4 Writing Basic Functions
Hussam Ghunaim, Ph.D.
Learning Objectives
At the end of this chapter, you will be able to
- Use many of the pre-defined functions from various C++ libraries
- Write your own user-defined functions
- Differentiate between different types of functions, like void functions and functions that return values
Pre-Defined Functions
Functions can be thought of as containers that contain code inside them. You have been using only one function in all programs written so far, called the main function. This was ok, as all the programs you wrote were relatively small. However, imagine if you need to write larger programs that contain hundreds or even thousands of lines of code. These programs will be very hard to review, debug, and modify. That is the reason why you must think of your code as built of various small pieces.
This way of thinking will perfectly match the algorithmic way of thinking. When you first write an algorithm to solve a certain problem, usually every task or step in the algorithm is translated into one function. In this chapter, you will learn to write and call many more functions called user-defined functions. Nevertheless, many other functions are already written and available for us to use right away, called pre-defined functions. These functions are saved in larger containers called libraries.
All functions written in C++ follow the same format:
returnType functionName(parameterType parameterName) {
//body of the function
}
To use functions correctly (either pre-defined or user-defined), you must understand very well the types of parameters[1] (if any), the function expects to have, and the returned type as well. If a function is defined to accept a string parameter, but you call it with a numeric type, like int or double, an error message will be thrown. Similarly, knowing the returned type of a function is important because, generally, you need to declare a variable to hold the returned value. For example, if you call a function that returns a char type, you must declare a variable with the same type to save the returned value.
Functions can have zero or more parameters included inside the parentheses that appear after the function name. If a function takes more than one parameter, a comma must be used to separate the parameters from each other. Example 3 shows this case. Every parameter added must be preceded with it is type. Additionally, functions must have a return type except if it does not return any value. In this case, the return type must be replaced by the keyword void. This topic will be discussed further in the upcoming section.
Table 1 shows some common pre-defined functions and their corresponding libraries. From the Table, you can learn that to call a function, you must use the parentheses associated with its name. These parentheses are used to pass any needed arguments[2]. Later in this chapter, when you start defining your own functions, you will notice that most functions need more information passed to them as arguments to perform their desired operations. Some functions do not need any arguments to work; however, it is still required to write empty parentheses associated with the name of the function. This is particularly important for the compilers to distinguish between the function name from any other variable name in the code.
| Standard Library | Function Name | Function Description | Examples | |||
| Arguments Types (if needed!) | Returned Type | How to call the function | Returned value | |||
| cmath |
sqrt | Calculates the square root of the given parameter. | double | double | sqrt(25.0) | 5.0 |
| pow | Raises the first parameter to the power of the second parameter. | double | double | pow(5.0 , 2.0 ) | 25.0 | |
| ceil | Finds the smallest integer greater than or equal to the given parameter value; however, the returned type is double! | double | double | ceil(1.1) | 2.0 | |
| floor | Finds the smallest integer less than or equal to the given parameter value; however, the returned type is double! | double | double | floor(1.7) | 1.0. | |
| round | Rounds decimal numbers to the nearest integer value. When the fractional part is less than 0.5, it is rounded down. Conversely, when the fractional part is 0.5 or greater, it is rounded up. | double | double | round(4.45) round(4.5) |
4.0 5.0 |
|
| cstdlib | abs | Finds the absolute value of the given parameter. | int | int | abs(-12) | 12 |
| rand | Generates pseudorandom integer values. It typically generates integer values in the range 0 to RAND_MAX, where RAND_MAX is a constant defined in the <cstdlib> library. The exact value of RAND_MAX may vary depending on the implementation. | void | int | rand() | values range from 0 to RAND_MAX | |
| srand | Passes a seed value to the rand function. | unsigned int | void | srand(10) | none | |
Unsigned Types:
Notice in Table 1, srand function expects an unsigned int as the argument type. In C++, unsigned types are integer types that can only represent non-negative numbers. This is in contrast to signed types, which can represent both positive and negative numbers. The keyword unsigned is used to declare unsigned types.
Table 2 compares the common signed and unsigned types in C++ along with their corresponding ranges. One advantage of using unsigned types is that to provide larger ranges whenever you need such a large range to solve problems.
| Type | Size (bits) | Size (bytes) | Minimum Value | Maximum Value |
|---|---|---|---|---|
| char | 8 | 1 | -128 | 127 |
| unsigned char | 8 | 1 | 0 | 255 |
| int | 32 | 4 | -2,147,483,648 | 2,147,483,647 |
| unsigned int | 32 | 4 | 0 | 4,294,967,295 |
| long int [3] | 64 | 8 | -9,223,372,036,854,775,808 | 9,223,372,036,854,775,807 |
| unsigned long int [4] | 64 | 8 | 0 | 18,446,744,073,709,551,615 |
To understand how unsigned types can provide larger ranges, we can recall that numbers are represented in computer memory as binary numbers. That is, if we have only 1-bit to represent numbers, then we can only represent two numbers, namely 0 and 1. If we choose to use 2-bits, then we can have four numbers, 00, 01, 10, and 11. By noticing the pattern, we can see that the number of possibilities equals 2n, where n is the number of bits used. For example, in Table 2, when raising 2 to the power of 8 bits, you will get the range of numbers available for the unsigned char type (notice that we start counting from 0). Similarly, you can calculate the range for unsigned int and long int by raising 2 to the power of the corresponding number of bits. On the other hand, signed types need to take one bit to represent the sign (usually 0 means positive and 1 means negative). That is, in the case of a signed char, 1 bit will be used to represent the sign, leaving 7 bits to represent the range; hence, the range now will split into two halves. One half represents the positive range starting from 0, and the other half represents the negative range. Similarly, for the signed int and long int, you can recalculate the range after taking away 1 bit to represent the sign and raising 2 to the power of the remaining bits.
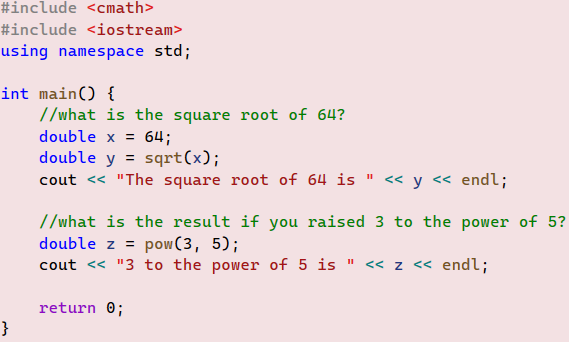
Example 01
Run the following code and notice how sqrt and pow functions are used.
rand function is used to generate pseudorandom numbers, which means not real random numbers. Random number generators use mathematical formulae to calculate these numbers; hence, they are predictable. However, their use is generally acceptable in many applications since pseudorandom numbers have statistical properties similar to true random numbers. Random number generators use a seed value to generate random numbers, which results in a specific set of random numbers for every seed value selected. If you need to generate a different set of random numbers every time a program runs, you need to find a way to randomly choose different seeds. Example 2 explains how you can do that.
Example 02
Run the provided code and notice that you are getting the same set of random numbers every time you run the code. To get a different set of random numbers, remove the double forward slash characters '//' to activate line 6 and run srand(5) function.
Although you get a new set of random numbers, they are also the same every time you run the code. If you want to get a different set of random numbers every time you run the code, you need to provide a different seed value to the srand function for every run.
The easiest way to do this is by calling the pre-defined time function. This function returns the system’s current time in seconds. This value can be used as the seed value. To see how this works, replace line 6 with this code: srand (time (0)); and run the code several times.
Notice how the time function has been passed as an argument to the srand function. Remember to include the <ctime> library to be able to use the time function.

Exercise 01
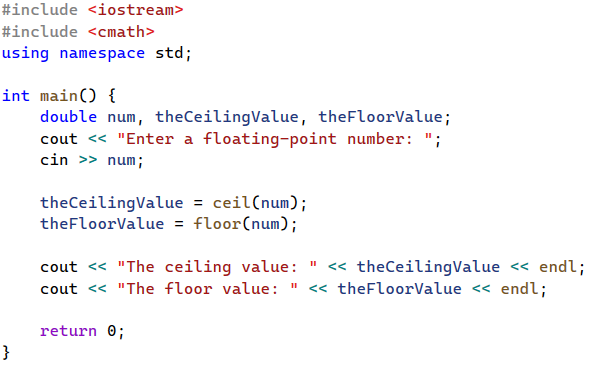
Write a program that asks a user to enter a floating-point number (a number with decimals) and prints the ceiling and floor values of that number using the pre-defined functions ceil and floor.
Exercise 02
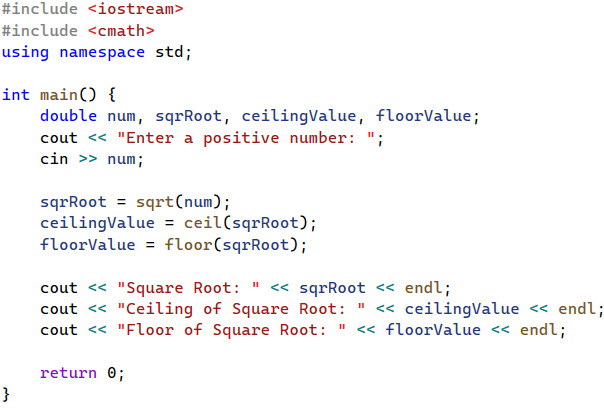
Write a program that asks a user to enter a positive number and prints the square root, ceiling, and floor values of that number using sqrt, ceil, and floor functions.
User-Defined Functions
Writing functions in C++ involves two steps: function declaration and definition. You can not use a function before it has been declared and defined. Otherwise, the compiler will complain that it is not able to execute the called function. Another restriction is that you cannot define a function inside another function. That is, every function must be declared and defined independently from any other function. There are two methods to declare and define functions.
Method 1:
First, you have to declare the function prototype above the main function. The function is called a prototype at this point because it is still not functional. The function still needs to be defined.
Second, define the function by writing all necessary code inside the body of the function below the main function.
Example 03
Declare and define a function called average that accepts two parameters of type int and returns the average of type double.
Answer
Let us use the general syntax for writing functions,
returnType functionName(parameterType parameterName) {
//body of the function
}
First, we declare the average function above the main function.
double average(int num1, int num2); //the function prototype or header
Second, define the average function below the main function.
double average(int num1, int num2){
double ave = (num1 + num2)/2.0;
return ave;
}
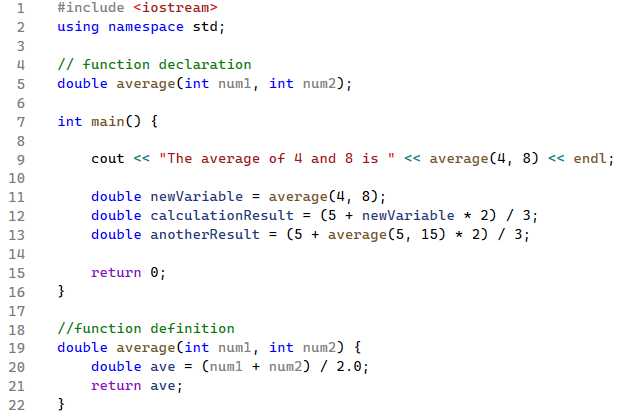
The following code is the complete example code. Note the positions where the average function is declared and then defined. Once the new function is declared and defined, it is now ready to be called. You can call functions in a similar manner to how you would call any other variable name. Lines 9, 11, and 13 show several ways to call the average function. It is important here to visualize how the code is executed. When you run this code, the execution will start from the beginning until it reaches line 9. When the average function is called, the execution will jump to the definition of the function in line 19 and execute its body. When the function completes its execution, the execution will go back to line 9, where it was exactly stopped, and continue from there. The same process happens when the function is called again in lines 11 and 13.
Method 2:
If you really do not like to declare functions and then define them, it is possible to immediately define functions above the main function without the need to declare them first.
Exercise 03
Write a function called add that takes two double parameters and returns their sum. Declare the function prototype at the top of your code and define the function below the main. In the main, call the add function with the arguments 10.05 and -7, and store the result in a variable. Print the result to the screen.
Exercise 04
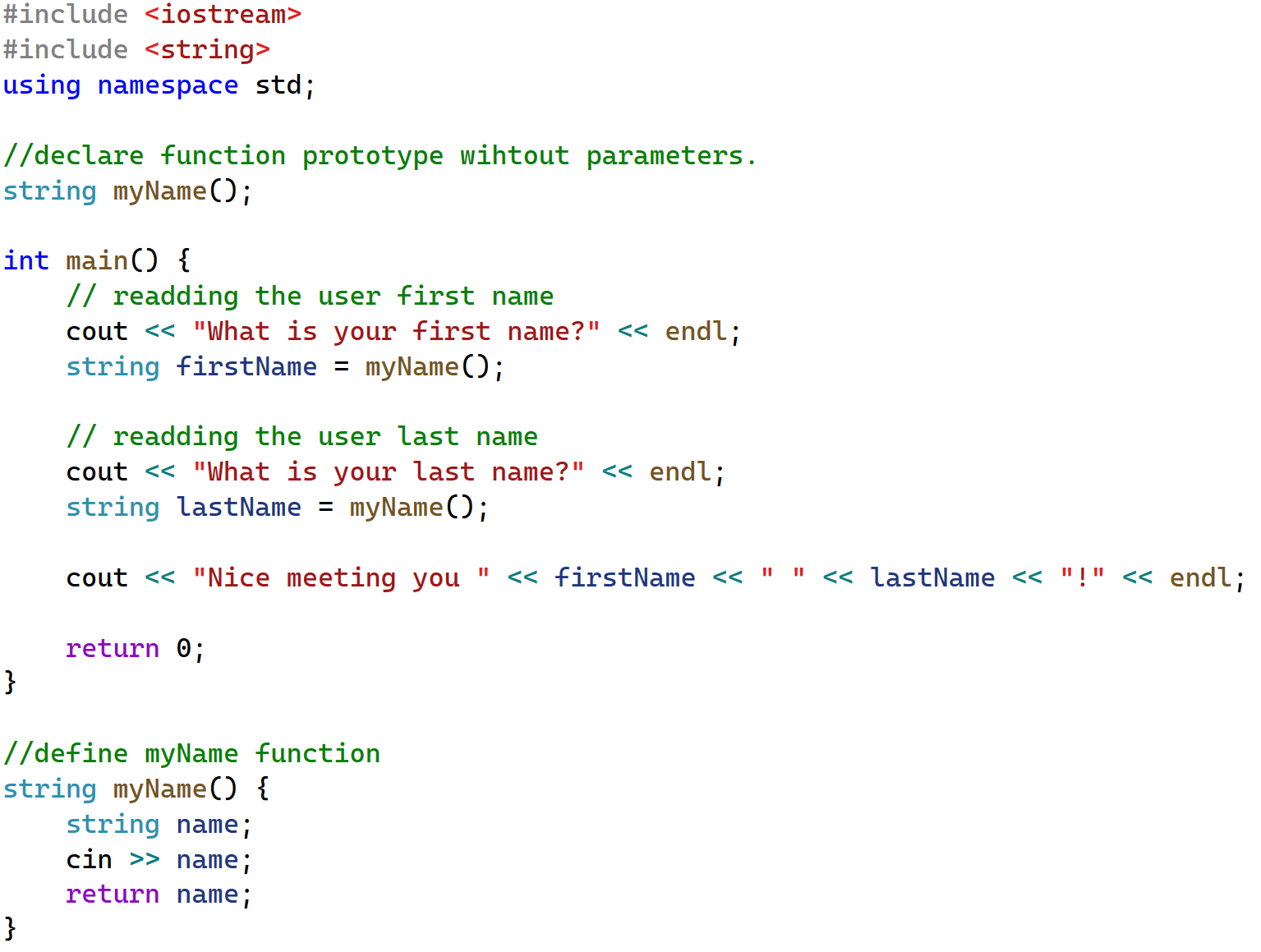
Write a function called myName that takes no arguments. The function should read the user name from the console and return it back to the caller. In the main function, myName must be called twice, one time to read the user's first name, and then the second call is to read the user's last name. The main function must print to the screen the following message: "Nice meeting you firstName secondName!".
Exercise 05
What is the difference between declaring and defining functions in C++?
Preconditions and Postconditions
Writing meaningful comments is one of the essential skills in software engineering. For first-time programmers, it is an even more crucial skill to focus on and practice. Therefore, in this book, you will frequently be asked to provide appropriate comments in the code. In Chapter 2, preconditions and postconditions comments were introduced and are reemphasized here. In these comments, programmers describe what functions expect to receive and what they are expected to return. If they are well-written, you can use the function confidently without issues because you know how to work with the function. Writing well-formatted comments is a very common practice in designing and developing software.
Example 04
Write precondition and postcondition comments for a function that calculates the square root of a number.
Answer
// precondition: the given number x must be a non-negative number.
// postcondition: the square root of x will be calculated and returned.
Example 05
Write precondition and postcondition comments for a function that calculates the factorial of a number.
Answer
// precondition: the given number n must be a non-negative.
// postcondition: the factorial of n will be calculated as follows: n! = 1 X 2 X .. X (n-2) X (n-1 ) X n.
Exercise 06
Write precondition and postcondition comments for the following function headers:
-
double calculateHypotenuse(double leg1, double leg2);
-
bool isLeapYear(int year);
-
bool isValidEmailAddress(string email);
-
double calculateMonthlyPayment(double principal, double interestRate, int loanTerm);
-
double calculateCirclePerimeter(double radius);
-
double kilometersToMiles(double kilometers);
-
bool isValidEmail(string email);
Numeric Functions
Functions can be written to satisfy almost any need or requirement. In this section, the focus will be on functions that perform a set of calculations and return the result back to the caller.
In example 4, you have written the precondition and postcondition for the square root function. Let us now develop the code for it. Calculating the square root of a positive number can be done through various algorithms. Here we will use a simplified algorithm called the Babylonian Algorithm. This algorithm iteratively approximates the square root. Note that this iterative method is an approximation and may not provide the exact square root.
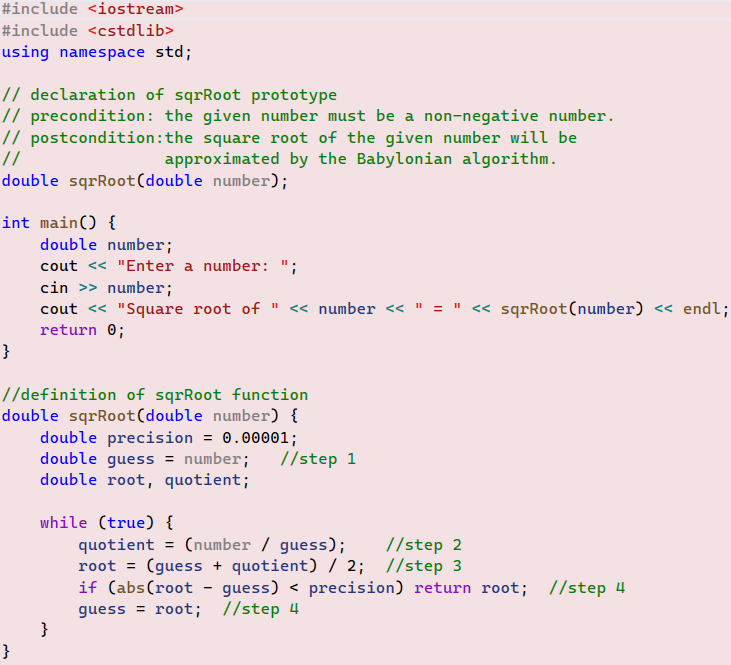
Example 06
Write a function that takes any positive number as a parameter and returns its square root using the Babylonian algorithm.
The Babylonian Algorithm:
- Step 1: Make an initial guess for the square root of the given number. This can be any positive number. For simplicity, we will let the
initial guess = given number. - Step 2: Divide the given number by the
guessto get thequotient. - Step 3: Average the
guessand thequotientto get a new guess. Let us call it theroot. - Step 4: If the absolute value of the difference between the
rootandguessis less than the precision value, return the current value of therootas the acceptable square root, otherwise, update the guess value and repeat steps 2, 3, and 4.
The code:
In example 5, you have written the precondition and postcondition for the factorial function. Let us now develop the code for it.
Example 07
Write a function that takes an int as a parameter and returns its factorial.
The Algorithm:
Calculating the factorial of any positive number is quite simple and straightforward. All that we have to do is create a loop that multiplies integers starting from 1 and incrementing by 1 up to the required number. This formula can help us visualize this procedure: n! = 1 X 2 X .. X (n-2) X (n-1 ) X n.
In designing solutions, giving examples is very helpful as well:
0! = 1 // by definition
1! = 1
2! = 1 X 2 = 2
3! = 1 X 2 X 3 = 6
4! = 1 X 2 X 3 X 4 = 24
.. and so on.
The code:
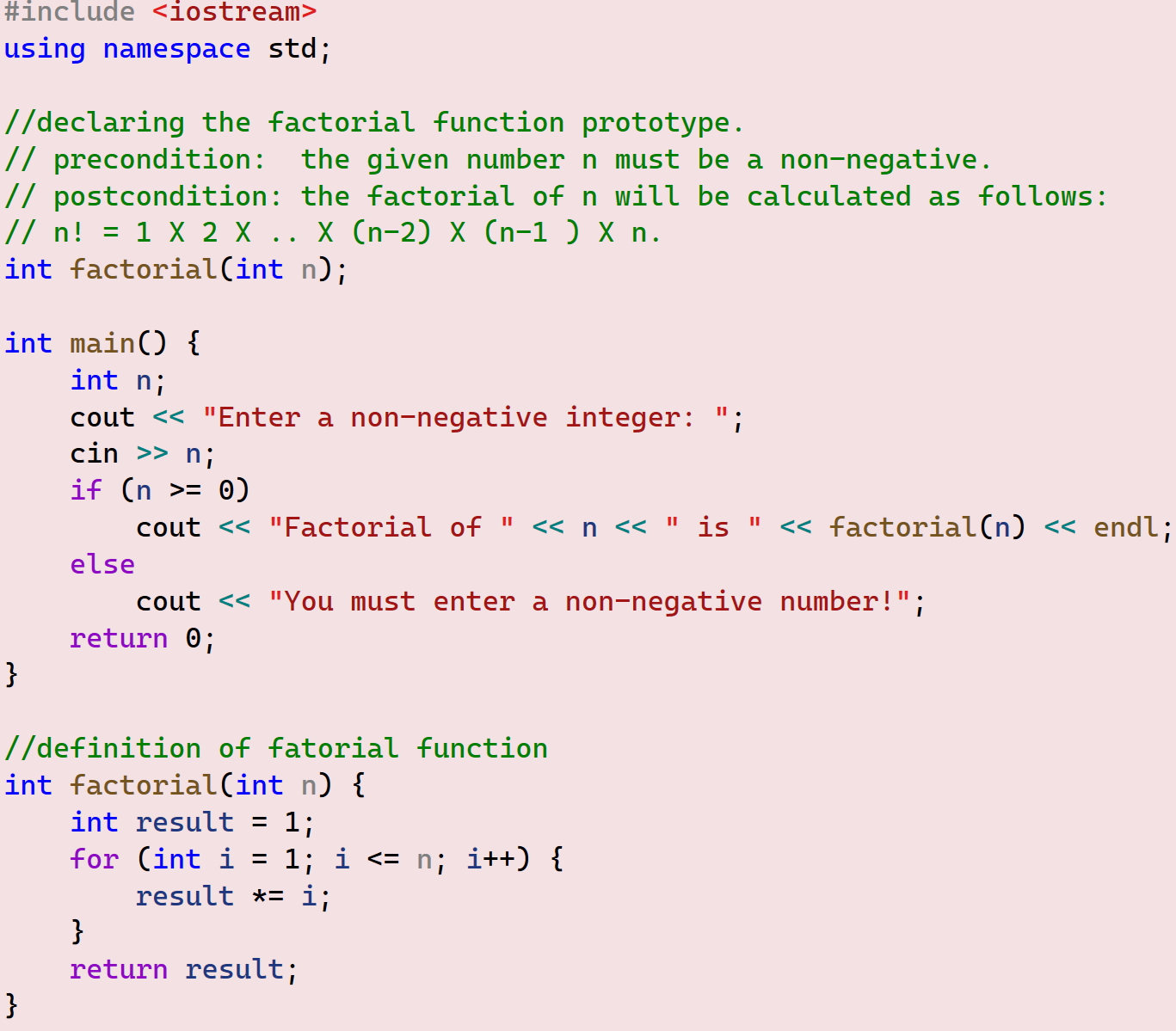
Test the provided code for several n values like 5, 10, and 20. What do you notice?! This code will be able to provide accurate results up to factorial 12. If you entered values for n larger than 12, surprisingly, you will get unreasonable results, like either negative numbers or zero! The problem here comes from the int type that, in most C++ implementations, has a size of 4 bytes (32 bits).
This means that any variable declared with the int type will be capable of holding integers ranging from -2,147,483,648 to 2,147,483,647. This range represents the positive and negative values that can be stored in a signed 32-bit integer using two's complement representation. The most significant bit is used to represent the sign of the number, leaving 31 bits for the magnitude. Therefore, for n > 12, the code will cause a memory overflow, resulting in unexpected outcomes.
There are some specialized libraries that can help in solving this problem. However, here we can partially solve this problem with a larger type than int, which is long long int. This type uses 8 bytes to be saved in the memory and can hold numbers ranging from -9,223,372,036,854,775,808 to 9,223,372,036,854,775,807.
Exercises 07
Modify the code in example 07 by replacing the type int with long long int. What is the largest n you can correctly calculate n! for it on your system?
Exercise 08
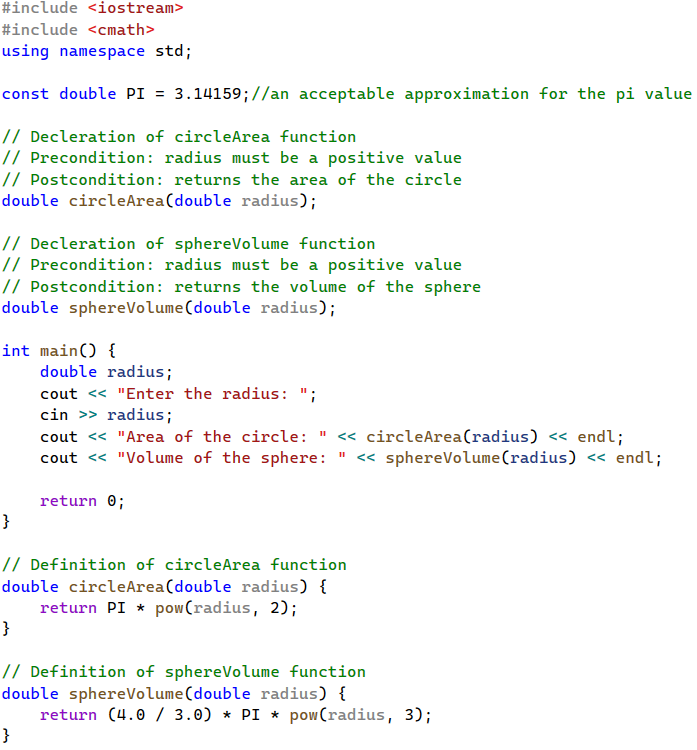
Write a program that asks the user to enter a radius value. Then, the main function will call two functions, circleArea, and sphereVolume, to calculate the area of the circle and volume of the sphere using the given radius. Both functions take one parameter of type double and return a double result. The code must have adequate preconditions and postconditions comments.
\[ \text{Area of the Circle: } A = \pi r^2 \]
\[ \text{Volume of the Sphere: } V = \frac{4}{3} \pi r^3 \]
Boolean Functions
Some functions are designed to help us in making decisions. Rather than including the needed logic in the main function, for clarity, we can delegate this job to another function to do so. Study the following examples and notice how Boolean functions can be used mainly as testing functions.
Example 08
Write a function that takes an int number and returns true if the number is even, otherwise, it returns false.
bool isEven(int num) { return num % 2 == 0; }
Example 09
Write a function that takes a char variable and returns true if the character is a vowel, otherwise, it returns false.
bool isVowel(char ch) { ch = tolower(ch); return ch == 'a' || ch == 'e' || ch == 'i' || ch == 'o' || ch == 'u'; }
Note: This function uses a pre-defined function tolower from the <cctype> library. Intuitively, this function converts any upper-case letter to a lower-case letter.
Exercise 09
Write a function that returns true if a number has five digits, otherwise, it returns false.
Exercise 10
Sometimes, we can use Boolean functions to enhance the code readability. For example, consider the following code:
The if-statement condition can be hard to read and contribute to the overall complexity of the code. Alternatively, we can move this condition into a Boolean function with an appropriate name: if ( checkEligiblity() ). The checkEligiblity() function will return either true or false to the if-statement.

Rewrite the given code by implementing the checkEligiblity() function.
NOTE: Practically, we might want users to enter values for GPA, SAT, and status variables. For the sake of simplicity, we hard-coded those values in this exercise.
Exercise 11
True or False:
- A function that returns a Boolean value can have multiple return statements throughout its body.
- A Boolean function in C++ cannot take parameters.
- The return type of a Boolean function can be any data type.
- A Boolean function can call other functions within its body.
- A Boolean function can be used as a while loop condition.
void Functions
void functions are a special type of functions that do not return any value back to the caller. However, to comply with the compiler requirements, we must add the keyword void as a placeholder in place of the regular type. void functions are useful when your needs are basically performing actions rather than calculations.
Example 10
Define a void function that takes a user name as a string type and prints a welcome message to the console.

Note in example 10 that void functions do not have a return statement. This makes sense as void functions are not supposed to return any values. However, adding the return statement does not cause errors. Additionally, if the user enters their full name or full name with a middle initial, the code will only print out the first name. This is because the stream extraction operator >> reads input until a whitespace is encountered, effectively using spaces to separate different values. If you want to read everything the user enters, you can replace the code cin >> name; with getline(cin, name);. The predefined getline function reads the entire line and saves it in the name variable. Be sure to include the <string> library to be able to use this function.
Example 11
Write a void function called printTable that takes two double parameters, num1 and num2, and prints them to the console formatted in a table shape. In the main function, the square and cubic roots will be calculated and passed to the printTable function.

Exercise 11
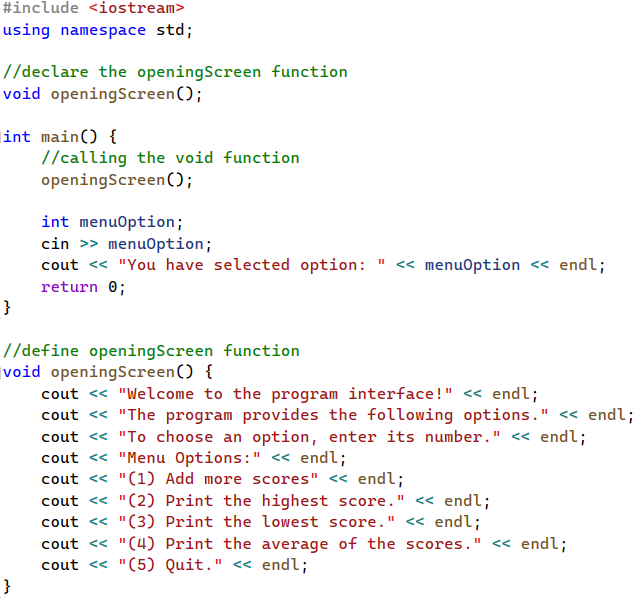
Write a void function called openingScreen that takes no parameters. The function's purpose is to provide information to users on how to use the program. Below is what the function has to print to the console.
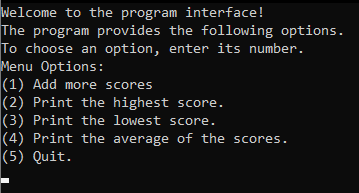
In the main function, call openingScreen function and write code to read user's choice. You do not need to implement any of the menu options.
Exercise 12
True or False:
- void functions always return a value.
- void functions can have parameters and arguments.
- void functions can be called from other functions.
- void functions must always have a return statement.
- void functions can be used to perform complex calculations and print them on the screen.
Wrap up!
In this chapter, you've delved into the world of functions in C++, exploring both pre-defined and user-defined functions. You've learned that functions serve as containers for code, allowing for better organization and reusability in your programs. With user-defined functions, you can break down complex tasks into smaller, manageable pieces, enhancing readability and maintainability. Pre-defined functions, housed in libraries, provide a wealth of functionality ready for use in your programs. You've gained an understanding of function syntax, including parameters, return types, and function prototypes. Additionally, you've explored Boolean functions for decision-making and void functions for actions without return values. Through exercises and examples, you've honed your skills in writing, declaring, and calling functions, setting the stage for more advanced programming concepts ahead. As you continue your journey in C++, remember that functions are powerful tools in your programming arsenal, empowering you to write clear, efficient, and scalable code.
Answers Key
Exercise 01:
Exercise 02:
Exercise 03:

Exercise 04:
Exercise 05:
In C++, a function declaration, also known as a function prototype, provides the compiler with information about the function’s name, return type, and parameters. It does not include the function’s body. A function declaration typically appears at the top of a source code file. However, a function definition includes both the function’s prototype and its body. The body of the function contains the statements that define what the function does. A function definition typically appears at the bottom of a source code file.
Exercise 06:
1.
Exercise 07
The modified code will calculate n! correctly up to n = 20 on my system.

Exercise 08:
Exercise 09:
bool isFiveDigits(string num) { bool result = true; if (num.length() != 5) result = false; return result; }
Exercise 10:

Exercise 11:
- true
- false
- false
- true
- true
Exercise 11:
Exercise 12:
- False
- True
- True
- False
- True
End of Chapter Exercises
- Write a function that converts Fahrenheit temperature degrees to Celsius using this formula: Celsius = (Fahrenheit - 32) * 5/9. The function should take a double parameter and returns a double. Add appropriate preconditions and postconditions comments. Hint, in C++ coding, the fraction 5/9 will result in 0 (why?!). To avoid this logical error, you should use 5.0/9.0 instead.
- In exercise 1, add a while loop to ask users if they wish to do another conversion.
- In exercise 2, the while loop condition must be a bool function that returns true if the user wishes to repeat the calculation; otherwise, the function will return false to terminate the loop.
- In Geometry, the distance between two points in the Cartesian Coordinate System is calculated by: \[ \text{distance =} \sqrt{{(x_2 \: - \: x_1)^2 + (y_2 \: - \: y_1)^2}} \] Write a function that asks users to enter the values
x1, x2, y1, y2,and returns the distance between the two points. Round the result to the nearest integer. Add appropriate preconditions and postconditions comments. - Write a function that takes a string as input and returns an int that represents the number of vowels in the string.
- Write a program that calculates the sum of all even numbers between 1 and 100. The program must use a Boolean function isEven that returns true if a number is even, otherwise, it returns false.
- Write a bool function that checks whether a given year is a leap year or not. The function takes one int parameter representing the year value and returns true if the year is a leap year; otherwise, it returns false. You must include appropriate preconditions and postconditions comments describing the implemented algorithm. This is a good practice if you intend to share your code and want to be sure that other developers will understand how you solved the problem at hand. It would be helpful to conduct some research to gain a better understanding of the reasons behind the occurrence of leap years and their importance in calendar tracking.
The Algorithm:
Step 1: If the year is evenly divisible by 4, continue to step 2; otherwise, return false
Step 2: If the year is evenly divided by 100, continue to step 3; otherwise, return true
Step 3: If the year is evenly divisible by 400, return true; otherwise, return false
Thus, years such as 1996, 1992, and 1988 are leap years because they are divisible by 4 but not by 100. Years that are divisible by 4 and by 100 but not by 400 are not leap years. However, years that are divisible by 4, 100, and 400 are leap years, such as years 1600 and 2000.
- Write a function that checks if a given sentence is a palindrome. A palindrome sentence is a sentence that reads the same forwards and backwards, considering only alphanumeric characters and ignoring spaces, punctuation, and capitalization. Do not forget the preconditions and postconditions comments to explain your algorithm.
Examples of Palindrome Sentences:
Madam, in Eden, I'm Adam.
Step on no pets.
Never odd or even.
Was it a car or a cat I saw?
No lemon, no melon.
- Write a void function that takes a string parameter and prints its reverse.
- Write a void function drawGraph(int rows) that prints a random number of * for every row it draws. A user must be allowed to choose how many rows they want to be drawn by passing an integer to the function argument. The total number of * printed on every row must not exceed 100. Below is a sample output:
Hint: You need to use nested loops to solve this problem.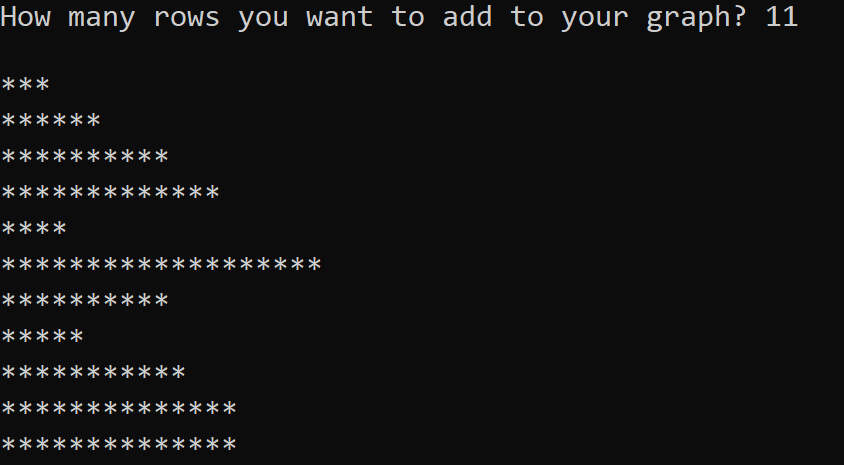
Projects
Project 1: Write a program that simulates a simple calculator.
- The calculator should have the following functions: add, sub, div, mul, squareRoot, power, repeat, and menu.
- For the first four functions, users must be able to enter as many numbers as they want by calling a Boolean function called repeat that takes no parameters. The repeat function must recognize the responses, y, Y, yes, and Yes. If a user enters anything else, it will be considered as no.
- Use predefined functions to implement the squareRoot and power functions.
- For the div function, add code to prevent the error of dividing by zero.
- Menu is a void function that prints a list of options users can choose from to perform the desired calculation.
- All functions must have adequate preconditions and postconditions comments.
Project 2: The metric system and the American system (also known as the Imperial system) are two different systems of measurement used in different parts of the world.
- Write a program that converts values from one system to another.
- Each of the provided conversions must be implemented in a separate function.
- The program must have a Boolean repeat function that allows users to perform conversions as often as they want.
- The program must have a void menu function that prints menu options for users to choose from.
- All functions must have adequate preconditions and postconditions comments.
Length:
- 1 meter (m) = 3.281 feet (ft)
- 1 kilometer (km) = 0.6214 miles (mi)
- 1 centimeter (cm) = 0.3937 inches (in)
- 1 millimeter (mm) = 0.03937 inches (in)
Mass/Weight:
- 1 kilogram (kg) = 2.205 pounds (lb)
- 1 gram (g) = 0.03527 ounces (oz)
Volume:
- 1 liter (L) = 0.2642 gallons (gal)
- 1 liter (L) = 33.814 fluid ounces (fl oz)
- 1 cubic meter (m^3) = 35.3147 cubic feet (ft^3)
Temperature:
- To convert Celsius (°C) to Fahrenheit (°F): Multiply by 9/5 and add 32.
- To convert Fahrenheit (°F) to Celsius (°C): Subtract 32 and multiply by 5/9.
Project 3 Rock, Paper, Scissors: Read Project 2 from Chapter 3 again and redo it by allowing a player to play against the computer. That is, you have to add code that randomly selects one choice from the three available choices (rock, paper, scissors). Redesign the project by writing a couple of suitable functions rather than adding all the code in the main function as you did in Chapter 3.
- Parameters are the variables declared in a function definition. They define the types and order of values that the function expects to receive when it is called. Parameters act as placeholders for the actual values that will be passed as arguments. ↵
- . Arguments are the actual values that are passed to a function when it is called. They correspond to the parameters defined in a function declaration. Arguments provide the specific values that will be used in the execution of a function. ↵
- The exact type size depends on your system and compiler. ↵
- The exact type size depends on your system and compiler. ↵

