6 Arrays
Hussam Ghunaim, Ph.D.
Learning Objectives
At the end of this chapter, you will be able to :
- Use Arrays to solve real-world problems
- Pass Arrays as Parameters for Functions
- Search and Sort Arrays
- Use Multi-dimensional Arrays to solve real-world problems
Introducing Arrays
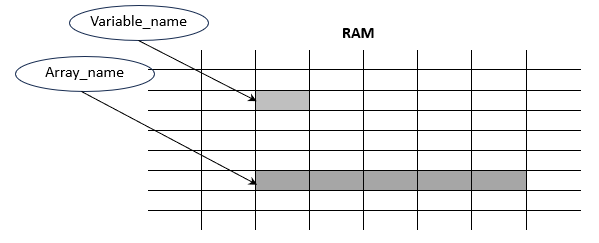
Figure 01 in Chapter 2 shows what happens in the computer's main memory RAM when you declare a variable of any primitive type. Primitive types are perfect whenever you need to store a single datum. However, what if you need to store multiple data of the same type, for example, a couple of numbers, characters, or even strings and objects? In this case, declaring many variables to store every needed datum will be time-consuming and very difficult to work with.
The code below declares both a single-value variable and an array. The only difference is the use of brackets [ ] to indicate the number of elements the array will store, Figure 01.
int var;
int var[5];
After declaring an array, the next step is initialization. For a single-valued variable, the process is as straightforward as you’ve experienced. However, initializing arrays offers several methods.
The simplest method is to assign values directly to each slot in the array. But this raises a question: how do we specify the exact slot for a particular value? The solution lies in using indices to number each slot, which are automatically generated by the system upon array declaration. As Figure 02 illustrates, indices start at 0, meaning the highest index in an array is the array’s size minus one. We can then initialize the array slots as follows:
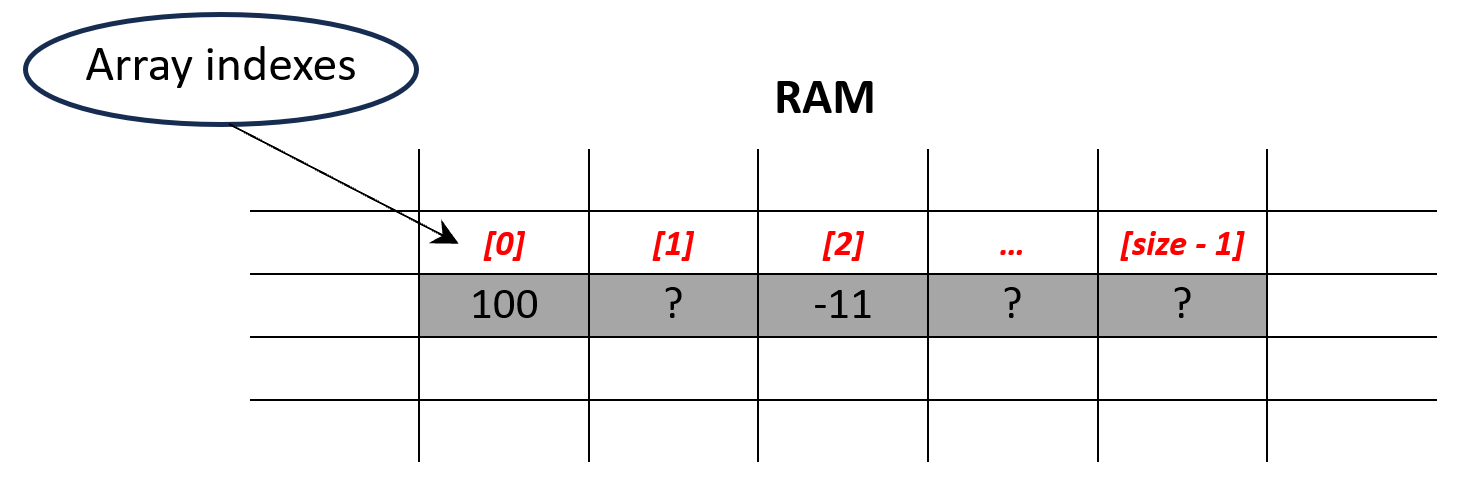
var[0] = 100;
var[2] = -11;
// and so on...
As demonstrated, it’s not necessary to fill all the slots in sequence; you can assign values as desired. However, it’s crucial to remember that upon declaration, all array slots are initially uninitialized. Accessing an uninitialized slot can lead to undefined behavior. If you choose to populate your array non-sequentially, you must keep track of which slots are filled and which remain unassigned. To prevent issues, you may want to initialize the entire array to default values at declaration. While this approach can be cumbersome for large arrays, using loops, as shown in Example 01, is often more practical.
Example 01
Run the provided code and comment on the results. The first thing you might notice is the use of a constant for the array size at the declaration. This is generally considered good programming practice because it enhances the code’s readability and modifiability. That is, if you decide to change the array size, you can do so in one location rather than modifying the size value throughout the code. Secondly, you can assign any desired value to any desired index in the array using the syntax myArray[i] = anyValue. However, ensure that the value you store is of the same type as the array, and the index does not exceed SIZE - 1. Lastly, you can access any value stored at the index i with the code myArray[i], assuming there is a value stored at that location; otherwise, you will get surprising outputs instead. One more thing to pay attention to is the for loop condition i < SIZE, which effectively ensures that the largest index value will be SIZE - 1.

Example 02
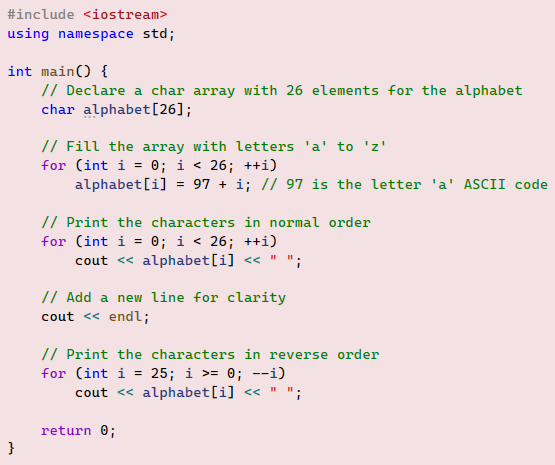
Run the provided code and comment on the results. In this example, we declare an array with a base type of char. The first loop fills the array with the 26 letters of the alphabet, starting from ‘a’ to ‘z’. In Chapter 2, we discussed type compatibility, where int and char types can be used interchangeably. Remember that characters are encoded with integer values following the ASCII standard encoding. Once again, pay attention to the loop condition i < 26, which will terminate the loop when the value of i becomes 26, to avoid an out-of-boundary error. The second loop does the opposite by printing out the contents of the array. The last loop prints the contents of the array in reverse order. Study this loop header carefully to understand how it works, noticing that the index values go from 25 down to 0.
Another method of declaring and initializing an array is as follows:
int anyName[5] = {4, 0, -11, 34, 7};
This code assigns each value to its corresponding place in the array, starting from index 0 and continuing up to index 4 in this example. Because the compiler can determine the size of the required array from the number of values provided for initialization, it is possible to omit the array size altogether:
int anyName[] = {4, 0, -11, 34, 7};Example 03
Run the given code and comment on the results. In this code, we use a variation of the for-loop called the for-each loop. This loop iterates through the array from start to end, conveniently eliminating concerns about index boundaries. The syntax for this loop is:
for (variable to hold each item in the array : array)
In this example, the loop variable is declared as a string to match the array’s base type. Note that at the beginning of the loop, the loop variable holds the first item in the array. With each iteration, the loop variable holds the next item, overriding the previously stored item, and so on until the last item in the array.

Exercise 01
Write a program that reads the user’s input of five numbers. The entered numbers can be positive or negative and can be either integers or decimals. The program must calculate and print out the average, sum, maximum (max), and minimum (min) of the entered numbers with appropriate formatting. To find the max, initialize the max variable to the smallest possible value on your system, typically -1e308, which is scientific notation for negative 10 raised to the power of 308. Then, compare each value stored in the array with this max variable, updating the max value whenever a new maximum is found. Use the same approach to find the min by initializing the min variable to the largest possible value, 1e308.
Exercise 02
Write a program that prompts the user to enter five words. The program should then print out the longest and shortest words entered.
Hint: In Chapter 2, you learned how to use some of the member functions of the string class, such as length(). You may want to reread that chapter to refresh your memory. For instance, to find the length of a string stored in a variable named word, you can use the expression word.length(). Similarly, when working with arrays, you can determine the length of a string stored at a specific index in the array with arrayName[index].length().
Passing Arrays as Function Parameters
Returning to the basic principle of robust programming, which involves dividing a program into several subproblems, each solvable by a single function, it’s essential that functions can accept arrays as parameters. The upcoming example will demonstrate how an array’s stored values can be accessed individually. Subsequently, another example will illustrate how an entire array can be passed to a function.
Example 04
Run the provided code and comment on the results. Lines 14 and 16 demonstrate how individual values stored in an array can be passed as parameters to a function. From the compiler’s perspective, it is looking for an integer parameter to match the squared function definition. So, when the expressions a[0] and a[3] are evaluated, they will be replaced by the values stored at those respective locations in the array. Similarly, in line 22, the compiler will attempt to resolve the expression a[ i ] to an integer value. If it fails, an error will be returned. Otherwise, the code can continue executing without any issues, provided that the expression a[ i ] always evaluates to a valid index within the defined array boundaries.
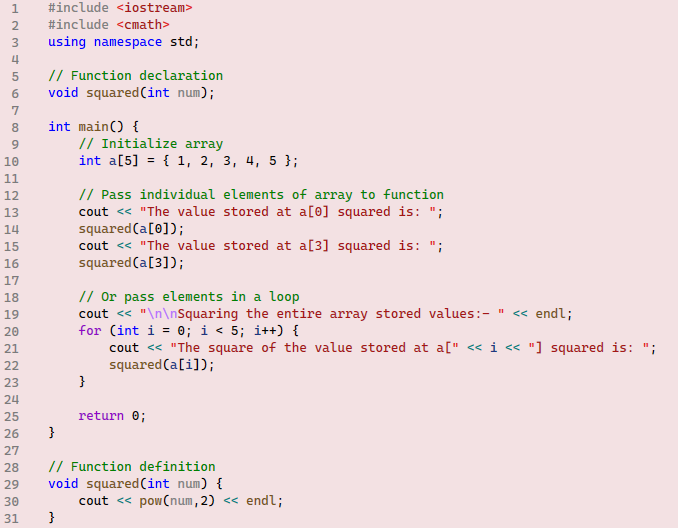
Example 5 demonstrates how to pass an entire array as a parameter. In Chapter 5, we discussed two methods of passing parameters: by value and by reference. However, passing arrays as parameters does not fall into either of these categories. For now, it’s acceptable to consider it similar to passing parameters by reference, but it’s important to note that it’s not exactly the same.
Example 05
Run the provided code and comment on the results. It is recommended to test the code several times to enhance your understanding and trace the results back to the code. When passing arrays to functions as parameters, it’s important to distinguish between the two different syntaxes.
Firstly, when declaring or defining a function, you must specify that the parameter is an array variable, as shown in line 4. In this example, we have only defined the userInput function at the top of the source file. However, if you choose to declare the function at the top of the source file and then define it at the bottom, you must ensure that the same syntax is followed in both the declaration and definition of the function.
Secondly, when calling the function in line 23, you should pass the array name without the square brackets [ ]. This is because the compiler already recognizes this variable as an array variable, as declared in line 21. Therefore, calling the function and passing the array name along with square brackets [ ] will cause an error, as it would appear as if you are declaring the array again.
Lastly, it’s necessary to pass the array size along with the array. This ensures that when accessing the array items, you do not go beyond the legal boundaries of the array.

Example 06
As always, it is important to run the code several times and trace the outputs back to the code for a better understanding of how the code works. This is a simple guessing game that utilizes two functions. The first function, initializeOcean, is used to initialize the array by placing a ‘1’ at a random location in the array to denote the ship (or anything else you’d like to symbolize). The rest of the array will be initialized to '0’s. The second function, playGame, asks users to enter their guesses from 0 to 9 and checks if they guessed correctly. Both functions take an array as a parameter. It’s important to distinguish between how the functions are defined and called in the code. break; statement is used in the second if statement in the while loop to terminate the loop once the user makes a correct guess. This makes sense as you do not want to keep asking users to enter more guesses if they have already guessed right. As a practice, delete the break; statement to see the effect it causes. Do not forget to put it back when you are done testing.

On a side note, using continue; statement in a loop skips the current iteration and proceeds to the next iteration. If there are any statements in the loop after the continue; statement, they are not executed for the current iteration. The break; statement, on the other hand, terminates the entire loop. Once a break; statement is encountered, the control exits the loop, and no further iterations are performed. As a practice, replace break; statement with continue; in the previous example to examine the effects. Do not forget to put break; back when you are done testing.
Exercise 03
Write a simple adventure game as follows:
- The game has an array that stores these strings "Forest", "River", "Mountain", "Cave", "Desert".
- A printLocation function that takes two parameters, the array and an integer variable representing an index to print the current location of the player. Initially, the current location will be at index 0, which means at the "Forest".
- A playGame function that takes two parameters, the array and its size. The job of this function is to ask the user to enter one of these commands, which are actually strings: "forward", "backward", "quit". Depending on the user input, the function should either increment or decrement the array index and print the new location by calling the printLocation function.
- Users should be allowed to move linearly from one location to another. Overjumping is not permitted.
- The playGame function must have an infinite loop that will keep asking the user to enter their chosen command indefinitely until they choose "quit".
- The palyGame function must check for invalid user inputs commands.
- The main function should have minimal code for merely declaring and initializing the array and calling the playGame function.
Exercise 04
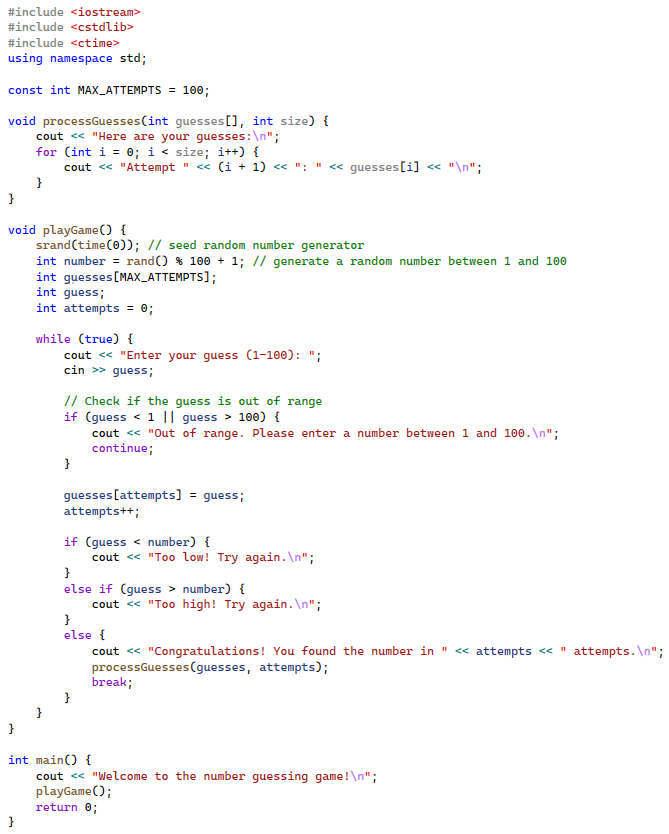
Write a simple guessing game as follows:
- The game has two helper functions.
- A playGame function that takes no parameters. The tasks of this function are:
- Generate a random number between 1 and 100.
- Declare an integer array to store all guesses made by a user.
- An indefinite loop that will keep asking a user to make guesses until they guess right. To help users guess right, print one of these messages with every guess: "Too low! Try again" and "Too high! Try again".
- If a user enters a guess outside of the allowed range, an error message should be printed out and prompt the user to enter another guess.
- A processGuesses function that takes two parameters, the array and its size. This function should be called from the playGame function when the user hits a right guess to print out all guesses made.
- The main function should have minimal code for merely calling the playGame function.
Search and Sort Arrays
By now, you have gained good experience working with arrays. It’s time to explore how arrays can be instrumental in solving real-life problems. This section will discuss two fundamental problems in computer science: searching and sorting.
It’s hard to imagine any software that doesn’t incorporate at least one, if not both, of these functionalities. We’ll begin with the simplest search algorithm, Linear Search, and then progress to a more efficient search algorithm, Binary Search.
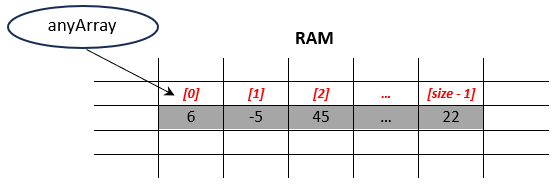
Linear Search
Figure 03 depicts an array named anyArray. To perform a linear search, all we need to do is compare the value we are searching for, which we’ll call target, with every value stored in the array starting at index 0: target == anyArray[0];
If the condition returns true, we’ve successfully found our target. If not, we increment the index and perform the next comparison, target == anyArray[1]. If the condition now returns true, that means we’ve found our target. Otherwise, we continue incrementing the index until we either find the target or reach the end of the array. At that point, we can print a message stating that the target does not exist in anyArray.
Example 07
The code is straightforward and self-explanatory. For a better understanding, modify the target value to include both existing and non-existing values in the array. This will allow you to test whether the code behaves as expected in both scenarios.

Example 08
Execute the code with various values for the bookName variable, including both existing and non-existing values in the array, to test the code’s behavior in both scenarios. In this example, the linearSearch function is responsible for executing the linear search, adhering to the best programming practices of having functions perform only one specific task. Additionally, note that the array is passed to this function as a constant array using the const modifier, line 5. Although this is not required, it also aligns with best programming practices. The linearSearch function is designed to perform a linear search without modifying the array contents. To safeguard the array from any accidental changes, the const modifier is used. Consequently, any attempt to modify the array within the linearSearch function will result in an error or, at the very least, a warning in most compilers. However, the modification on line 27 will not cause any errors as it is executed in the main function, which does not have any restrictions on modifying the array contents.

Using the modifier const with arrays can become tricky. In C++, if an outer function is declared to receive a const array as a parameter and it calls an inner function, the inner function must also be declared to receive a const array. This is because the const modifier promises that the function will not modify the array. If the inner function were allowed to modify the array, it would contradict this promise. Therefore, to ensure the integrity of the const promise, any function that is passed a const array must also promise that any inner function it calls will not modify the array contents.
Exercise 05
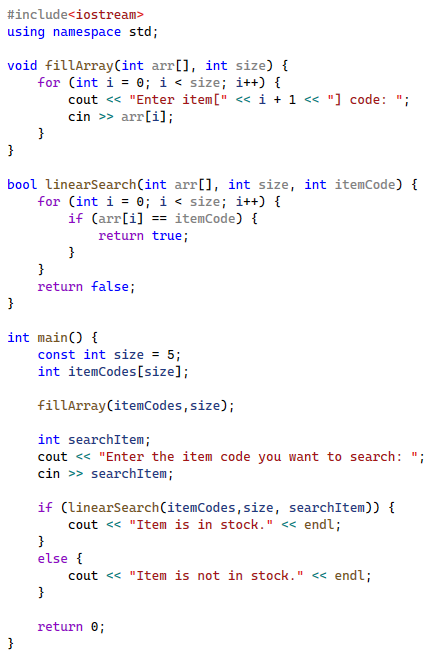
A store manager needs to check whether an item exists or not in their store. To assist with this, write a program that implements the following functions:
- A void fillArray function that takes 2 parameters, the array and its size. This function task is to fill the array with the item codes that the user enters.
- A bool linearSearch function that takes three parameters: the array, the array size, and an item code. The function returns true if the code is found in the array; otherwise, it returns false.
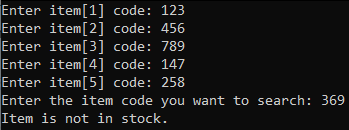
Figure 04: Sample output of the required program. - In the main function, an array to store the item codes is created. For simplicity, create an int array that can store five item codes. The main function should print out appropriate messages depending on what the linearSearch function returns to announce the outcomes of the search.
Use the attached output sample as guidance, Figure 04.
Exercise 06
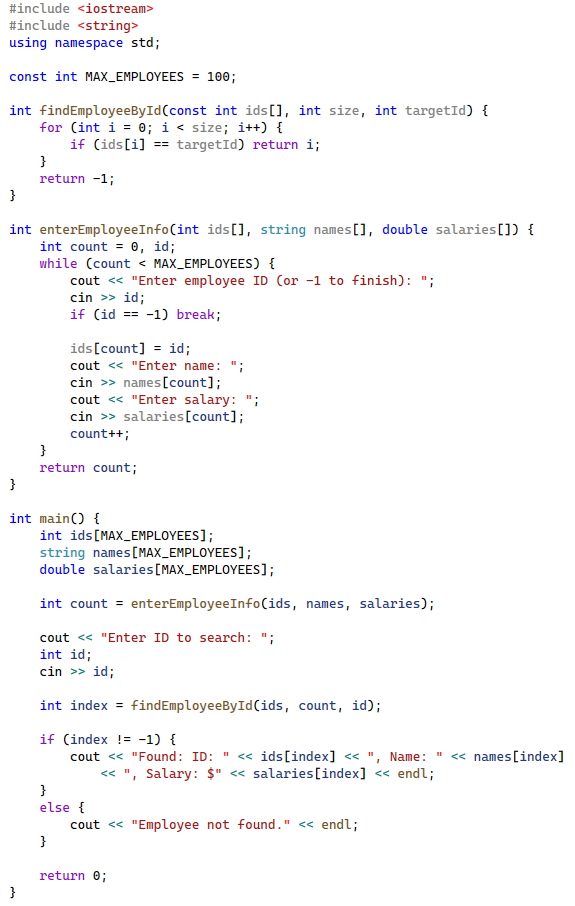
A simple Employee Management System. The program should allow users to enter employee information (ID, name, and salary) and search for employees by their ID. Users should be able to input as many employees as they want up to the maximum number allowed. To keep the code simple, the code only needs to read employees' last names (one word). Your implementation should include the following components.
- A constant MAX_EMPLOYEES is set to 100.
- A function findEmployeeById that performs a linear search on an array of employee IDs.
- A function enterEmployeeInfo, that allows users to input employee data (ID, name, salary) and store it in three separate arrays.
- A main function that:
- Declares three arrays for employee IDs, names, and salaries with appropriate types.
- Calls enterEmployeeInfo to populate the arrays.
- Prompts the user for an ID to search.
- Uses findEmployeeById to search for the employee.
- Displays the found employee's information or a 'not found' message.
Binary Search
The binary search algorithm is significantly more efficient than the linear search. For instance, consider an array with 1,000,000 elements. In the worst-case scenario, a linear search would require 1,000,000 comparisons to either find the target or determine that the target does not exist in the array. In contrast, the binary search algorithm can accomplish the same task with only 20 comparisons, which is [latex]\boldsymbol{\mathit{\log_2(1,000,000)=20}}[/latex]!! The base-2 logarithm is used because of the way the algorithm operates. In each step of a binary search, the algorithm halves the size of the search space. This is achieved by selecting the middle element and discarding either the left half or the right half of the search space. Consequently, the number of steps it takes to reduce the search space from n elements to 1 is equivalent to the number of times you can divide n by 2 until you reach 1.
Binary Search Algorithm
- Start with a Sorted Array: Binary search requires the array to be sorted in ascending or descending order. If the array is not sorted, we must sort it first.
- Find the Middle Element: Calculate the middle index of the array. This can be done by adding the start index and the end index of the array and then dividing the sum by 2. If this division results in a fractional number, decide whether to round up or down.
- Compare the Middle Element with the Target Value:
- If the middle element is equal to the target value, then we have found the target and the search is complete.
- If the middle element is greater than the target value (in an ascending sorted array), then the target must be in the left half of the array.
- If the middle element is less than the target value (in an ascending sorted array), then the target must be in the right half of the array.
- Repeat the Process: If the target is not found, repeat the process with the appropriate half of the array (either left or right, depending on the comparison in Step 3).
- End Condition: The search ends when the target is found or when the start index is greater than the end index, which means the target is not in the array.
Example 09
Run and test the provided code for several target values. To solidify your understanding, trace the results back to the code to understand how it actually finds the correct results with the help of Figure 05. As usual, the binarySearch function takes three parameters: the array, its size, and the target.
Because the Binary Search algorithm keeps halving the array, we need to track the start and end indices for each chosen half. Figure 05 shows that at the beginning, the start index is 0, and the end index is set to 9, following the code in line 7. The while loop condition will keep checking whether start is smaller or equal to end. When this condition fails, it means the array size is reduced to 0 without finding the target. At this point, line 23 executes and returns -1.
Otherwise, the while loop will start its first iteration by calculating the middle index value on line 10, which is middle = (0 + 9) /2 = 4.5. However, the middle variable type was declared as int. In other scenarios, this should be considered a logical error. However, in this particular example, it is used to get rid of the fraction part of the division as the indices must be integers. Therefore, the middle variable is set to equal 4.
In the if-else statements, we check three possible scenarios: line 13 checks if the value at the calculated middle index equals the target. If this is true, then line 14 returns the index to announce that the target is found. Otherwise, the second condition checks whether the value at the calculated middle index is smaller than the target. If this is true, we can ignore the entire lower half of the array because we know that the array is sorted in ascending order and it is impossible to find the target in that half. Line 17 modifies the start index accordingly. On the other hand, if this condition returns false, then we can conclude the opposite, which is that the target must be in the lower half of the array. Line 20 modifies the end index accordingly.
Figure 5 shows the while loop iterations that will lead to the position where the target exists. The binarySearch function will return either the index where the target is found or -1 to indicate that the target was not found. Based on what the binarySearch function returns, the main function will print the appropriate message.


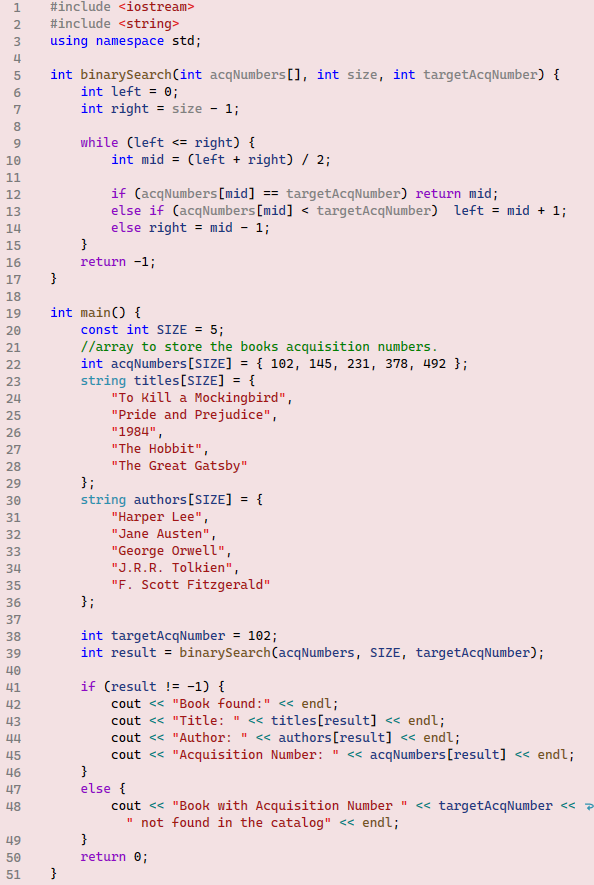
Example 10
Run and test the provided code for several target values (note that line 48 must be entered as one line). In this example, we can examine how the binary search algorithm can be useful in solving real-world problems. For instance, national public libraries’ catalogs can contain up to several million books. Searching such extensive catalogs necessitates very efficient search algorithms.
Study the code and notice how we removed all braces from the if..else statements. Since all branches have only one statement in them, there is no need for any braces. Additionally, we used three separate arrays to hold the books’ acquisition numbers, titles, and authors’ names.
In the following section, we will discuss multidimensional arrays. For now, it’s acceptable if we have to declare a couple of separate arrays.
Exercise 07
Write a program implementing a Binary Search algorithm to search a sorted array of words. Your implementation must include a binarySearch function that takes three parameters: the array of words, the size, and the target. This function must return either the index of the target if found, or -1 if the target word does not exist in the array. The main function should call the binarySearch function and print appropriate messages to the user based on what the binarySearch function returns.
Hint: In this exercise, you will compare words (i.e., strings) with each other. This is possible because characters are encoded according to the ASCII scheme. When comparing strings, you are actually comparing their ASCII codes character by character until a difference is found or the end of the string is reached.
Exercise 08
Answer these multiple-choice questions:
Question 1: What is the primary condition for applying a binary search algorithm on an array?
a) The array must be unsorted.
b) The array must be sorted.
c) The array must contain only positive numbers.
d) The array must contain unique elements.
Question 2: If an array has 1,000,000 elements, how many comparisons does the binary search algorithm need in the worst case to either find the target index or determine that the target does not exist in the array?
a) [latex]\boldsymbol{\mathit{\log_{10}(1,000,000)=20}}[/latex]
b) [latex]\boldsymbol{\mathit{\log_2(1,000,000)=20}}[/latex]
c) 0
d) It is impossible to know the answer
Question 3: Which of the following correctly initializes the left and right indices for a binary search?
a) int left = 1, right = size;
b) int left = 0, right = size;
c) int left = 1, right = size - 1;
d) int left = 0, right = size - 1;
Question 4: What does the binary search algorithm do if the middle element is equal to the target?
a) It returns the middle element.
b) It continues to search the right half of the array.
c) It returns the index of the middle element.
d) It continues to search the left half of the array.
Sorting Algorithms
There are several sorting algorithms in use. Their efficiency varies; however, we will discuss the simplest algorithm in this chapter, the Bubble-Sort algorithm.
Bubble-Sort Algorithm
- Compare the first element with the second element in the unsorted array.
- If the first element is larger than the second element, swap them; otherwise, no change is necessary.
- Repeat step 2 for each pair of adjacent elements until reaching the end of the array.
- At the end of step 3, the largest element will be at the last position in the array.
- Repeat steps 1 to 3 for the remaining unsorted portion of the array (i.e., from the first element to the last unsorted element).
- After each pass, the next largest element will be placed in its correct position, just before the previously sorted elements.
- Repeat step 5 until the entire array is sorted and no more comparisons are needed.
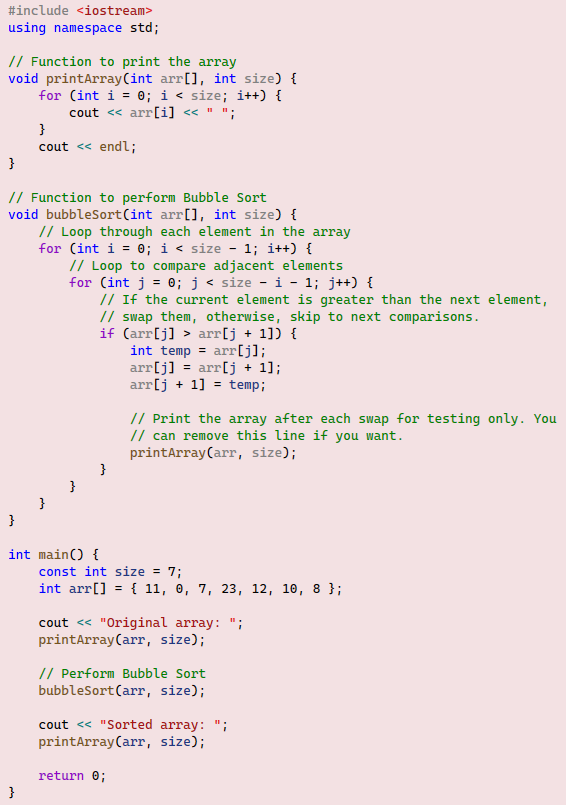
Example 11
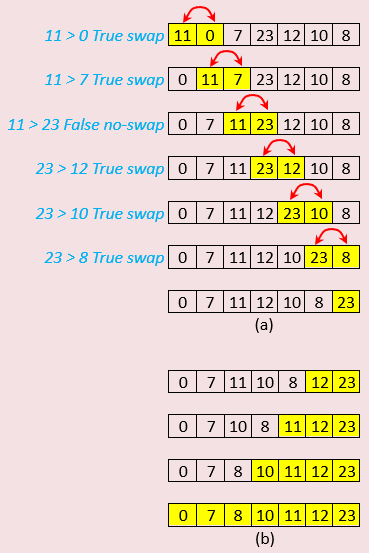
Run and test the provided code with several different array values. Be sure to carefully read and understand the Bubble Sort algorithm for smoother comprehension of this example. Figure 06 visualizes the algorithm's dynamics. At the heart of this algorithm, the largest values bubble up to the right of the array, effectively sorting the array in ascending order.
Figure 06(a) shows how the largest number in the array, 23, is placed in the last position at the far right. This process starts by comparing the first two positions of the array. The result of each comparison bubbles the larger number to the right. Initially, the number 11 was swapped with 0 and 7. Later, number 23 surpassed number 11 and swapped with the remaining values all the way to the rightmost position in the array. These comparisons and swaps are handled by an inner loop that compares every two adjacent elements using the condition arr[ j ] > arr[ j + 1 ]. It is crucial not to exceed the array's boundaries, so the inner loop condition j < size - i - 1 is used.
The condition j < size would normally stop the loop at the last position in the array. However, in this algorithm, we are comparing the last element with the element before it, requiring the condition to be j < size - 1. Additionally, we subtract i from size because, after placing the largest number at the last position in the array, we must exclude that particular element from comparisons in subsequent passes. Hence, the correct condition is j < size - i - 1. The inner loop passes through the entire array, but we also need an outer loop to keep the algorithm running for each element in the array. Therefore, the outer loop condition must be i < size - 1.
Figure 06(b) shows the effect of the outer loop on every element in the array, causing the array to be incrementally sorted at every iteration. Note that although the first three elements happen to be in sorted order, "0, 7, and 8", the loop will continue systematically running until all loop conditions are exhausted. While this is not the most efficient approach, the code can be modified to terminate early if needed.
Exercise 09
Modify example 11 code to sort an array of characters.
Exercise 10
Modify example 11 code to sort an array of strings.
Exercise 11
Answer the following multiple-choice questions:
Multi-Dimensional Arrays
Arrays are flexible enough to contain other arrays within them, creating what is known as Multi-Dimensional arrays. For simplicity, we will discuss only the 2-dimensional arrays. Visually, a 2D array resembles a table with rows and columns. Higher dimensions are technically possible but are more challenging to visualize or conceptualize.
The syntax to declare a 2-dimensional array is:
baseType variableName[rows];
int anArray[5][7];
This declaration creates an array with 5 rows and 7 columns. It's important to note that array indices start from 0. Therefore, the row indices range from 0 to 4, and the column indices range from 0 to 6.
Example 12
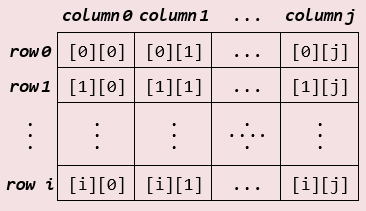
Figure 07 illustrates how 2-dimensional arrays (or simply 2D) should be visualized as sets of rows and columns. The challenge lies in addressing each location within this array. The solution is to use two indices: one for rows and another for columns. It's essential to remember that the first index refers to rows, while the second index refers to columns.
The provided code demonstrates how to declare and initialize the array in a single line. First, specify the number of rows and columns required for the array. Then, populate the array with values. Note how the code assigns values to the array row by row within curly braces, separated by commas except for the last row. To access any location in the array, you must specify the exact indices, as shown in Figure 07. Since multidimensional arrays are often large, nested loops are commonly used to access or modify values. Notice how the ranges of the outer and inner loops are structured to match the dimensions of the array and prevent out-of-bounds errors. For better comprehension, you can uncomment the second cout line inside the inner loop (and comment out the other cout line) to print the contents of the array along with their corresponding indices.

Example 13
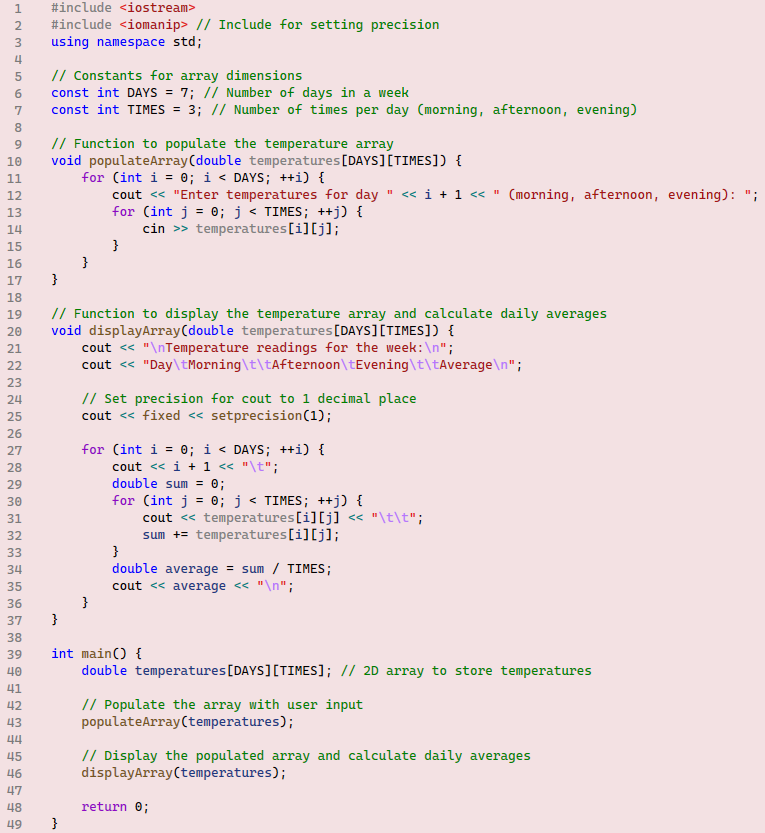
Run the code and trace the outputs for a better understanding. This step is crucial for comprehending how individual locations in a 2D array can be accessed. There are two functions in this example: populateArray, which allows users to enter daily temperatures, and displayArray, which prints the array's contents and calculates the daily temperature average.
The populateArray function takes a 2D array as a parameter, specifically of type double to store temperatures with decimals. As is typical with 2D arrays, it requires nested loops to access each location. In this implementation, locations are accessed row by row. Initially, the outer loop selects the first row (i = 0), and the inner loop iterates through each column (j = 0 to j < TIMES). This process repeats for each subsequent row until the outer loop terminates when i < DAYS becomes false. This allows the user to populate the entire array with daily temperatures for 7 days.
The displayArray function also takes the same array as a parameter to print its contents and calculate the daily temperature average. Using a similar nested loop structure, it iterates through rows with an outer loop and columns with an inner loop. Within the inner loop, line 32 sums the temperatures for the day, while in the outer loop, line 34 calculates the average temperature for each day. Line 35 prints the average. Line 25 uses fixed and setprecision(1) manipulators to ensure that all printed temperatures have only one decimal place. These manipulators, which will be discussed in detail in Chapter 7, are included from the <iomanip> library. The tab escape character \t is used in lines 22, 28, and 31 to format the output in a tabular shape.
The main function primarily declares the 2D array and calls the populateArray and displayArray functions.
Exercise 12
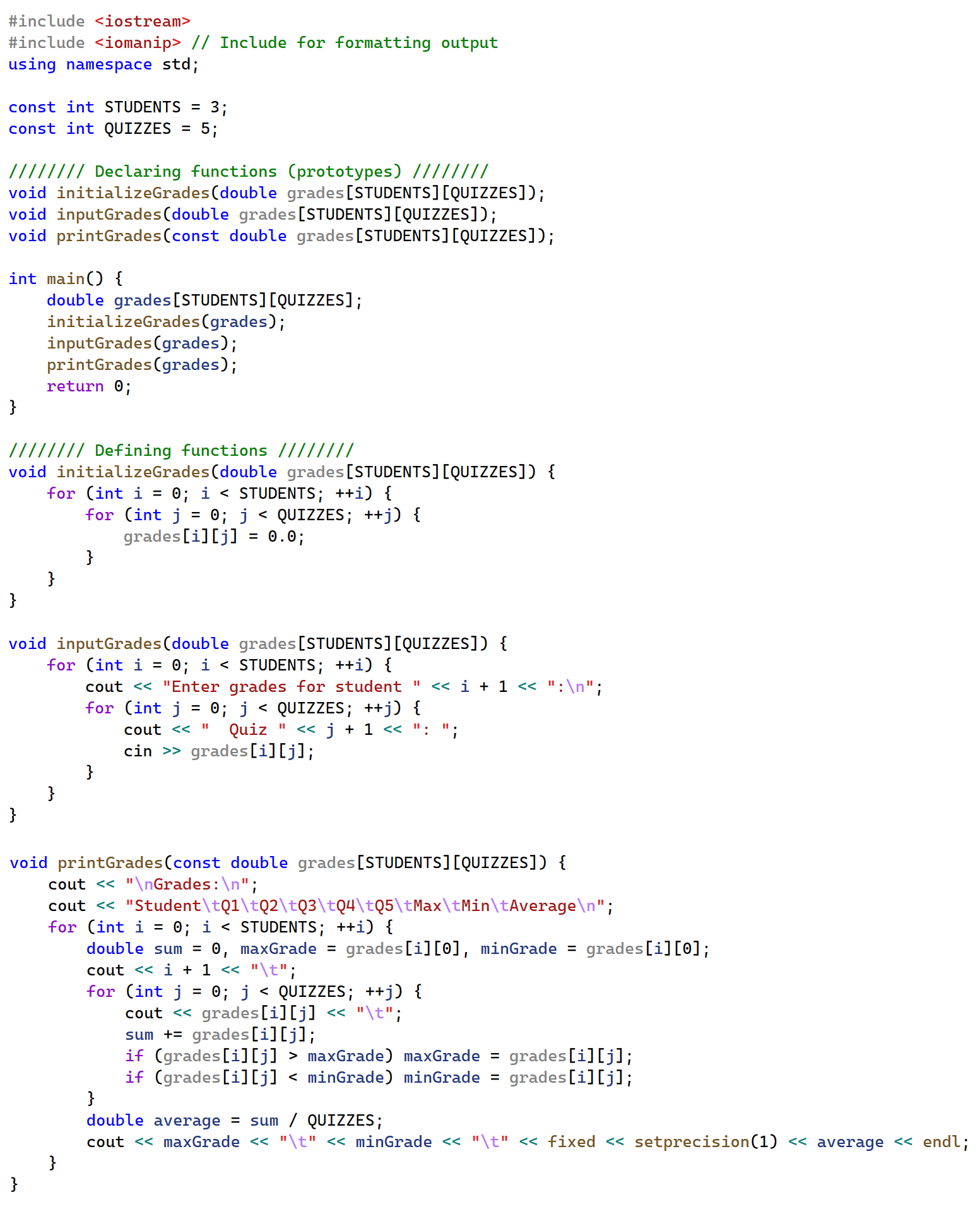
This exercise is similar to Example 13, so you can reuse some of its code. Write a program to enter students' grades and calculate the maximum, minimum, and average of these grades using 2D arrays. In this exercise, you must follow standard C++ coding best practices by first declaring all functions at the top of the file (above the main function) and then defining the functions below the main function. The program must include at least the following functions:
1) main: This function must have minimal code, primarily to declare the 2D array and call other functions.
2) initializeGrades: This function takes the 2D array as a parameter and initializes its entries with default values of its base type. Remember the importance of avoiding accessing any uninitialized memory locations, especially with large arrays, when it becomes difficult to track all memory locations.
3) inputGrades: This function takes the 2D array as a parameter and allows users to enter students' grades, which can be decimals. The number of students and the number of grades must be declared as constants.
4) printGrades: This function takes the 2D array as a constant parameter to prevent any accidental changes to its values. The tasks of this function are to find the maximum, minimum, and average grades, and then print all grades along with these statistics in a formatted tabular presentation. You can use the same manipulators used in Example 13.
Exercise 13
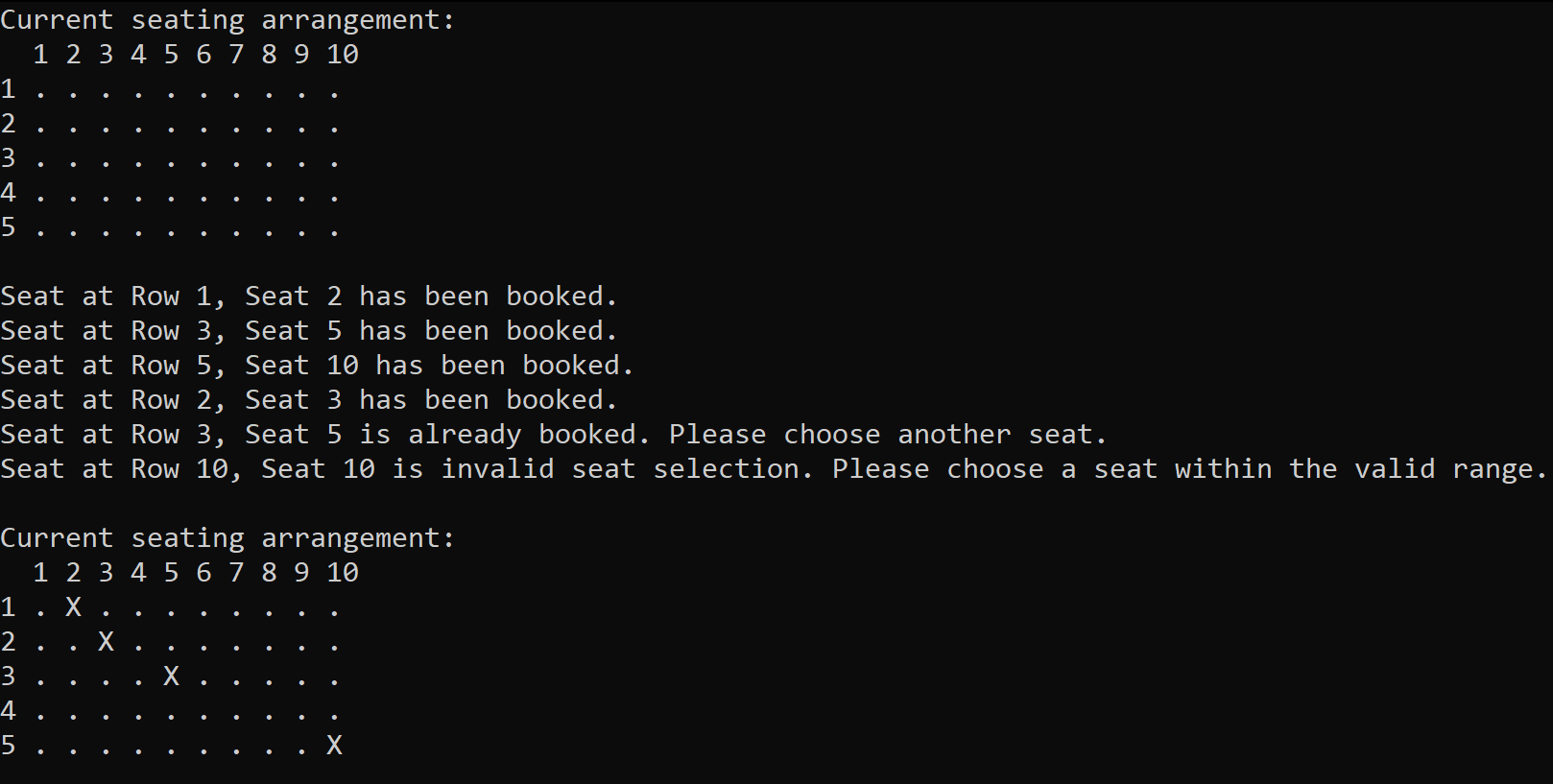
You are tasked with developing a program to manage seating in a movie theater using a 2-dimensional array. Each seat in the theater can either be available ' . ' or booked 'X'. Your program should print the current seating arrangement, allow the booking of seats, and handle invalid seat selections gracefully.
Program functions:
1) initializeTheater(): Initializes a 2-dimensional array (theater) to represent the seating arrangement. Initially, all seats are set to ' . ' to denote availability.
2) The theater array must be declared globally to ensure accessibility across all functions without passing it as a parameter.
3) printSeating(): Displays the current seating arrangement in a grid format, showing row and column numbers along with seat availability ' . ' or 'X'.
4) bookSeat(int row, int col): Books a seat specified by row and column numbers by checking if the seat is available ' . ', books it by changing the value to 'X'. This function must provide appropriate feedback for successful bookings, attempts to book already booked seats, and invalid seat selections.
5) main function: Contains minimal code, primarily calling other functions to simulate booking seats at various rows and columns. It should print the seating arrangement before and after each booking attempt to demonstrate changes in seat availability.
Note: Figure 08 shows a sample run of the program.
Wrap up
This comprehensive introduction to arrays covers a wide range of essential concepts and techniques. Starting with the basics, readers learn how to declare, initialize, and access elements in one-dimensional arrays. The material then progresses to more advanced array manipulation, demonstrating various methods for working with arrays, including using loops to populate and display their contents.
An important aspect covered is the passing of arrays to functions, highlighting the differences between passing individual elements and entire arrays. This knowledge is crucial for developing modular and efficient code. The text also delves into fundamental search algorithms, introducing both linear search for unsorted arrays and the more efficient binary search for sorted arrays. In addition, the Bubble Sort algorithm is explained as an example of how to sort array elements, providing a foundation for understanding more complex sorting techniques.
Multi-dimensional arrays are introduced, with a focus on 2D arrays. Readers learn techniques for declaring, initializing, and manipulating these more complex data structures. Throughout the material, various examples and exercises demonstrate real-world applications of arrays, such as storing temperatures, managing student grades, and implementing a simple theater seating system. These practical scenarios help reinforce the theoretical concepts and illustrate the versatility of arrays in solving diverse programming problems.
The content emphasizes important programming practices, including avoiding uninitialized memory access, using constants for array sizes, and properly structuring code with function declarations and definitions. By adhering to these best practices, readers can develop more robust and maintainable code. Overall, this material provides a solid foundation in array usage, equipping students with the necessary skills to tackle more advanced data structures and algorithms in their future studies.
Answer Key
Exercise 01:

Exercise 02:
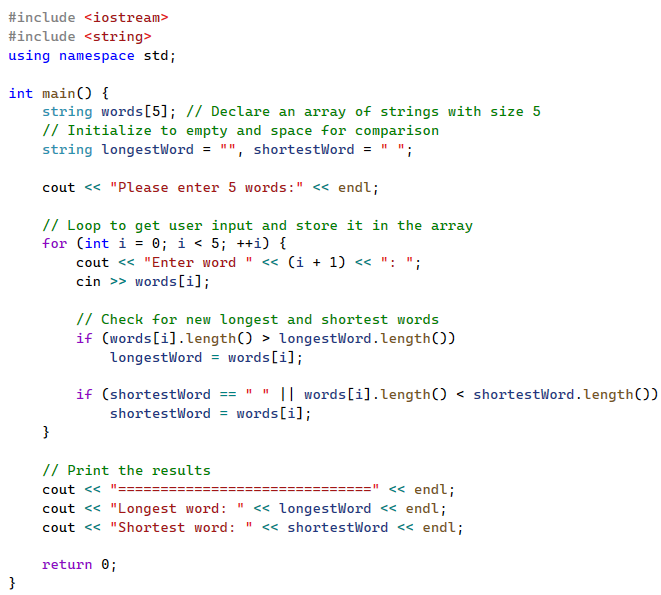
Exercise 03:
A sample solution:

Exercise 04:
A sample solution:
Exercise 05:
A sample solution:
Exercise 06:
A sample solution:
Exercise 07:
A sample solution:

Exercise 08:
Question 1: B
Question 2: B
Question 3: D
Question 4: C
Exercise 09:
The required changes are:
1) Declare an array of characters instead of an array of integers:
char arr[size] = { 'd', 'g', 'e', 'b', 'c', 'f', 'a' };
2) Change the printArray and bubbleSort functions' headers to take an array of characters as a parameter:
void printArray(char arr[], int size)
void bubbleSort(char arr[], int size)
3) Change the temp variable inside the if statement to a char type:
char temp = arr[j];
Exercise 10:
The required changes are:
1) Include the <string> library.
2) Declare an array of strings instead of an array of integers:
string arr[size] = { "Zara", "John", "Mike", "Alice", "Bob" };
3) Change the printArray and bubbleSort functions' headers to take an array of strings as a parameter:
void printArray(string arr[], int size)
void bubbleSort(string arr[], int size)
4) Change the temp variable inside the if statement to a string type:
string temp = arr[j];
Exercise 11:
Question 1: B
Question 2: C
Question 3: C
Question 4: D
Exercise 12:
A sample solution:
Exercise 13:
A sample solution:

End of Chapter Exercises
Multiple Choice Questions:
1) What is the correct way to declare an array of 5 integers?
a) int var(5);
b) int var{5};
c) int var[5];
d) int var = 5;
2) What is the index of the last element in an array of size 5?
a) 5
b) 4
c) 3
d) 0
3) Which loop is used in Example 03 to iterate through the array?
a) while loop
b) do-while loop
c) for loop
d) for-each loop
4) What is the benefit of using a constant for array size declaration?
a) It makes the code run faster
b) It allows for dynamic resizing of the array
c) It prevents resizing the array at runtime, which is not allowed in C++
d) It reduces memory usage
5) In C++, array indices start at:
a) 0
b) 1
c) -1
d) Depends on the array type
True/False Questions:
6) Arrays can store multiple types of data.
7) It's necessary to fill all array slots in sequence when initializing.
8) Accessing an uninitialized array slot can lead to undefined behavior.
9) The for-each loop eliminates concerns about index boundaries when iterating through an array.
10) In C++, you can omit the array size when initializing it with values.
Coding Questions:
11) Write a C++ code snippet to declare and initialize an array of base type of double with values 1.2, 2.98, 3.01, 4.33, and 5.5.
12) Write a for loop to print all elements of an integer array named "numbers" of size 10.
13) Declare a character array to store the alphabet (a-z) and initialize it using a for loop.
14) Write a for-each loop to print all elements of a string array named "words". Assume the array "words" is already declared and initialized.
15) Write a code snippet to find the maximum value in an integer array named "values" of size 5. Assume the array "Values" is already declared and initialized.
Multiple Choice Questions:
16) When passing an array to a function, how should you pass the array name?
a) With square brackets []
b) Without square brackets
c) With parentheses ()
d) With curly braces {}
17) What does the break; statement do in a loop?
a) Skips the current iteration
b) Terminates the entire loop
c) Restarts the loop
d) Has no effect on the loop
18) What does the continue; statement do in a loop?
a) Terminates the entire loop
b) Restarts the loop
c) Skips the current iteration
d) Has no effect on the loop
19) How is passing an array as a parameter different from passing by value or by reference?
a) It's exactly the same as passing by value
b) It's exactly the same as passing by reference
c) It's a unique category, different from both
d) It depends on the compiler
20) When passing an array to a function, what additional information is typically needed?
a) The size of the array
b) The memory address of the array
c) The data type of the array
d) The name of the array
True/False Questions:
21) Passing individual array elements to a function is the same as passing any other variable of the same type.
22) When calling a function with an array parameter, you should include the square brackets with the array name.
23) In C++, arrays are always passed by reference to functions.
Coding Questions:
24) Write a function declaration for a void function named processArray that takes an integer array and its size as parameters.
25) Write a code snippet that demonstrates how to pass an individual array element to a function named squareNumber.
26) Write a void function that takes an integer array of size 10 as a parameter and initializes it with random numbers between 1 and 100.
27) Write a function that finds and returns the index of a given value in an array, or -1 if the value is not found. Assume that the array stores integer values.
28) Write a function that reverses the order of elements in an array. Assume that the array stores integer values.
29) Write a code snippet to call calculateAverage function that takes a double array myArray and its size as parameters. The function should return the average. Do NOT implement the function.
Multiple Choice Questions:
30) What is the primary characteristic of a linear search algorithm?
a) It requires the array to be sorted
b) It compares the target with every element in the array sequentially
c) It divides the array in half repeatedly
d) It uses a hash function to locate elements
31) What does the const modifier do when used with an array parameter in a function?
a) It makes the array elements constant
b) It prevents the function from modifying the array contents
c) It allows the function to modify only certain elements of the array
d) It has no effect on arrays
32) In the context of the Employee Management System exercise, what does the findEmployeeById function do?
a) It adds a new employee to the system
b) It deletes an employee from the system
c) It performs a linear search on an array of employee IDs
d) It modifies an employee's information
True/False Questions:
33) In a linear search, each item in the array is sequentially compared to the target value until the target is found or the end of the array is reached.
34) When using const with array parameters, inner functions called by the outer function don't need to use const.
35) The linear search algorithm requires the array to be sorted before searching.
Coding Questions:
36) Write a function that implements a linear search on an integer array. The function should take three parameters (the array, its size, and the target) and return the index of the target if found, or -1 if not found. The function should not be able to modify any of the array values.
37) Re-implement the fillArray function described in Exercise 05 by filling the array with random 3-digit codes ranging from 100 to 999.
38) Write a function called countDuplicates that takes a character array and its size as parameters. The function's task is to determine if the array contains any duplicate characters and count the occurrences of these duplicates. The function must not modify the array contents.
39) Which of the following statements is true about binary search?
a) Binary search can be applied to either sorted or unsorted arrays.
b) Binary search can only be applied to arrays sorted in descending order.
c) Binary search divides the search space into two halves in each step.
d) Binary search can only be applied to arrays sorted in ascending order.
40) Why is the base-2 logarithm used in measuring the efficiency of the binary search algorithm?
a) Because the algorithm compares each element sequentially.
b) Because the algorithm halves the search space at each step.
c) Because the algorithm sorts the array first.
d) Because the algorithm multiplies the search space at each step.
41) Write a program that uses two arrays: one to store employee IDs and another to store employee names. Implement a binary search function to search the ID array. This function should return the index of the ID if found, or -1 if the ID doesn't exist. In the main function, create an indefinite loop that:
- Prompts users to enter an ID they want to look up
- If the ID is found, it prints both the employee ID and name
- If the ID is not found, it prints a message stating that the employee ID does not exist
- Terminates the loop if the user enters -1
Multiple Choice Questions:
42) What is the main characteristic of the Bubble Sort algorithm?
a) It sorts in descending order
b) It uses recursion
c) The largest (or smallest) values bubble up to the right of the array
d) It requires a separate array for sorting
43) In the Bubble Sort algorithm, how many elements are guaranteed to be in their correct position after the first pass?
a) All elements
b) Half of the elements
c) One element
d) Two elements
44) What is the condition used in the inner loop of the Bubble Sort algorithm to avoid exceeding array boundaries?
a) j < size
b) j < size - 1
c) j < size - i
d) j < size - i - 1
45) Why is the variable 'i' subtracted in the inner loop condition (j < size - i - 1)?
a) To speed up the sorting process
b) To exclude already sorted elements from comparisons
c) To reverse the sorting order
d) To count the number of swaps
46) What is the outer loop condition in the Bubble Sort algorithm?
a) i < size
b) i < size - 1
c) i < size + 1
d) i <= size
True/False Questions:
47) In Bubble Sort, the largest unsorted element is placed in its correct position after each pass.
48) The Bubble Sort algorithm always requires the same number of passes, regardless of the initial order of elements.
49) Bubble Sort can be modified to terminate early if the array becomes sorted before all passes are completed.
50) The inner loop in Bubble Sort compares every two adjacent elements in the unsorted portion of the array.
51) Modify the bubbleSort function in example 11 to stop early if the array becomes sorted before all passes are completed.
52) Write a function that uses the Bubble Sort algorithm to find the k-th largest element in an unsorted array.
Multiple Choice Questions:
53) When accessing elements in a 2D array, what does the first index typically refer to?
a) Columns
b) Rows
c) Depth of the array
d) Width of the array
54) What is the correct way to initialize a 2D array in C++?
a) int arr[][] = {{1,2}, {3,4}};
b) int arr[2][2] = {1,2,3,4};
c) int arr[2][2] = {{1,2}, {3,4}};
d) int arr[2,2] = {1,2,3,4};
55) What is the purpose of using nested loops with 2D arrays?
a) To sort the array
b) To access or modify values in the array
c) To create the array
d) To delete the array
True/False Questions:
56) The indices of a 2D array in C++ start from 1.
57) It's possible to have arrays with more than two dimensions in C++.
58) Using the 'const' keyword when passing a 2D array as a parameter prevents accidental modifications to the array.
59) Write a function to initialize a 2D array of size 3x3 with all elements set to 0.
60 ) Write a function to print the contents of a 2D array of size 3x3.
61) Write a function to find the sum of all elements in a 2D array of size 3x3.
62) Write a function to find the maximum element in a 2D array of size 3x3.
63) Write a function to transpose a 2D array of size 3x3 (swap rows with columns).
Projects
Project 01: Voting System
Overview
You will create a program that simulates a simple voting system. The program will generate random votes for a set of candidates, determine the winner based on the number of votes each candidate received, and display the results.
Steps to Follow
Include Necessary Libraries
- Use the <iostream> library for input and output functions.
- Use the <string> library to handle string data types.
- Use the <cstdlib> library for random number generation.
- Use the <ctime> library to seed the random number generator with the current time.
Generate Random Votes Function
Create a function that generates random votes for the candidates. The function should take an array of integers (to store votes), the number of candidates, and the number of votes to generate as parameters.
Use a loop to generate random votes and increment the vote count for a randomly selected candidate.
Find the Winner Function
Create a function that finds the candidate with the highest number of votes. The function should take an array of strings (candidates), an array of integers (votes), the number of candidates, and two reference parameters (winner and maxVotes) to store the result. Use a loop to compare the votes and update the winner and maxVotes variables accordingly.
Print Results Function
Create a function that prints the number of votes each candidate received and announces the winner. The function should take an array of strings (candidates), an array of integers (votes), the number of candidates, the winner, and the maxVotes as parameters. Use a loop to print the results for each candidate and display the winner.
Voting System Function
Create a function that sets up the candidates and votes arrays, generates random votes, finds the winner, and prints the results.
- Initialize an array of strings with the names of the candidates.
- Initialize an array of integers with zeros to store the votes.
- Call the function to generate random votes.
- Call the function to find the winner.
- Call the function to print the results.
Main Function
In the main function,
- Seed the random number generator with the current time.
- Prompt the user to enter the number of votes to generate.
- Call the voting system function with the number of votes.
Example Output
Welcome to the voting system!
Enter the number of votes to generate: 1000000
Generating 1000000 random votes for candidates: Alice, Bob, Charlie, Dave, Eve.
Alice received 200203 votes.
Bob received 200329 votes.
Charlie received 199176 votes.
Dave received 200157 votes.
Eve received 200135 votes.
The winner is 'Bob' with 200329 votes.
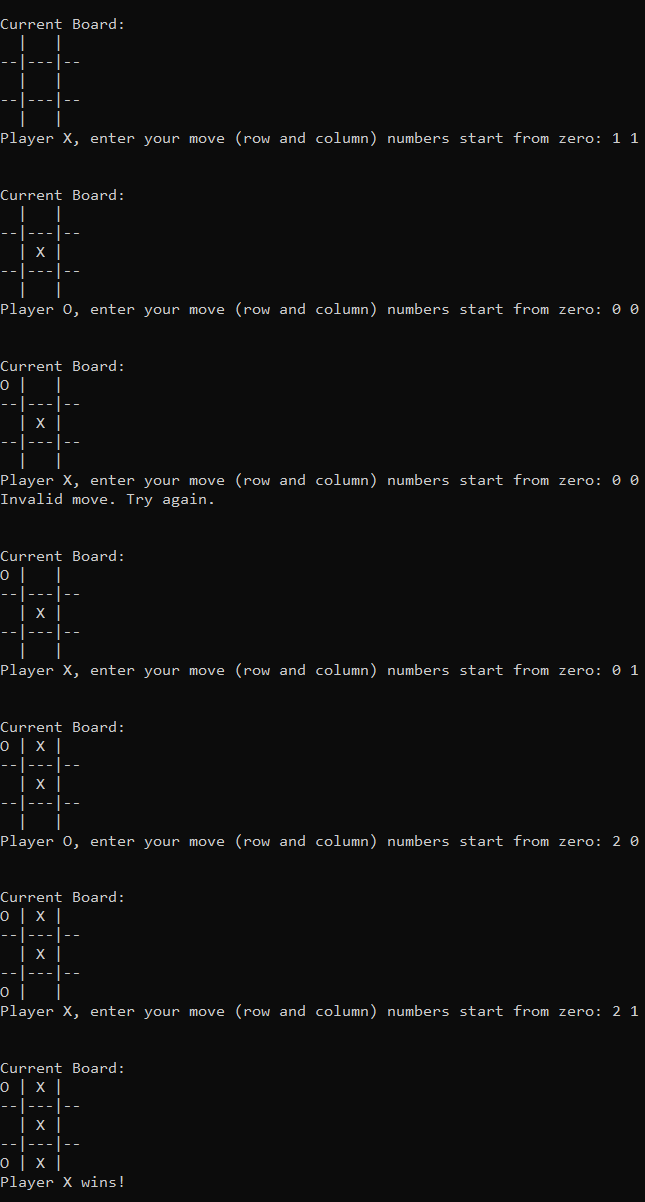
Project 02: A Simple X / O (Tic-Tac-Toe) Game
- How to work with 2D arrays: You'll create and manage a 3x3 game board using a 2D array.
- Basic control structures: You'll use loops and conditional statements to control the flow of the game.
- Functions: You'll break down the game logic into smaller, manageable functions.
- User input: You'll learn how to accept and validate user input for their moves.
- After each move, the program will :
- Update the game board.
- Check if the move resulted in a win using checkWin().
- If no one has won, check if the game is a draw using checkDraw().
- Switch turns between the players 'X' and 'O'.