9 Recursive Thinking in C++
Hussam Ghunaim, Ph.D.
Learning Objectives
Type your learning objectives here.
- Understands the recursion mechanism
- Write void recursive functions
- Write recursive functions that return values
Introducing Recursion
A recursive function, in simple words, is a function that calls itself. Initially, this might sound weird, but later, we will explore some scenarios where implementing recursive functions can be the best solution.
Example 01
 To clarify the idea of recursive functions, let us start by comparing an iterative code to a recursive code. When you run the given code, you will get a countdown from 3 to 0 twice. One output comes from the iterative code, lines 12 and 13. The second output comes from calling the countDown(3) function, line 16. As you can see, the output is identical; however, the implementation is entirely different. The iterative code is straightforward and self-explanatory. The recursive code, however, needs a careful explanation. First of all, when we say a function is allowed to call itself, this implies a possibility for an infinite loop unless we add some code to terminate the recursive calls at some point.
To clarify the idea of recursive functions, let us start by comparing an iterative code to a recursive code. When you run the given code, you will get a countdown from 3 to 0 twice. One output comes from the iterative code, lines 12 and 13. The second output comes from calling the countDown(3) function, line 16. As you can see, the output is identical; however, the implementation is entirely different. The iterative code is straightforward and self-explanatory. The recursive code, however, needs a careful explanation. First of all, when we say a function is allowed to call itself, this implies a possibility for an infinite loop unless we add some code to terminate the recursive calls at some point.
In line 16, when the countDown(3) is called, the value 3 will be passed to the function’s formal parameter in line 4. Next, line 5 prints the current value of the num variable, which is 3, and the if-statement in line 6 checks the condition num > 0. At this time, this condition returns true and causes a recursive call to the countDown function with the updated argument num – 1, which is 3 – 1 = 2. This time, 2 will be printed to the console, and the if-statement condition still returns true, causing a new recursive call countdown (2 -1). This pattern will keep repeating until the if-statement condition returns false, terminating the recursive calls.
To better understand example 01, let us visualize how recursion works. Figure 01 shows what happens when a function calls itself recursively. Every time a function calls itself recursively, a new frame for the function call will be created on the call stack in memory (RAM), exactly similar to a function that calls another function, except here, the function being called is itself. This is a primary reason why recursion often consumes more memory than iterative code. However, it provides effective solutions to some problems, which you will discover shortly.
Starting from the main() function, when countDown(3) is called, the system will invoke the function in memory and move the execution control to it. The first call will pass 3 as an argument. Then, inside the function, the code will run normally, that is, printing the current value of the argument num and checking the if condition num > 0, which returns true. Therefore, countDown function will be called again with the updated argument (3 – 1). Now, the execution will move over to the second copy of the countDown(2) function with the argument num value as 2. Execution will continue as normal until hitting the if condition again. This pattern will continue until the if condition returns false when the recursion terminates.
At this point, when the last created copy of the countDown(0) completes its execution, it will be terminated and removed from memory, as we expect it would happen with every function when it ends its execution. The execution control will return to the previous copy of the function, letting it continue its execution as well. This pattern will continue until the execution control returns to where it started in the main() function. Now, the main() function can continue its execution if there is any more code left before the main() function returns and is terminated and removed from memory as well.

Stacks to Manage Recursion
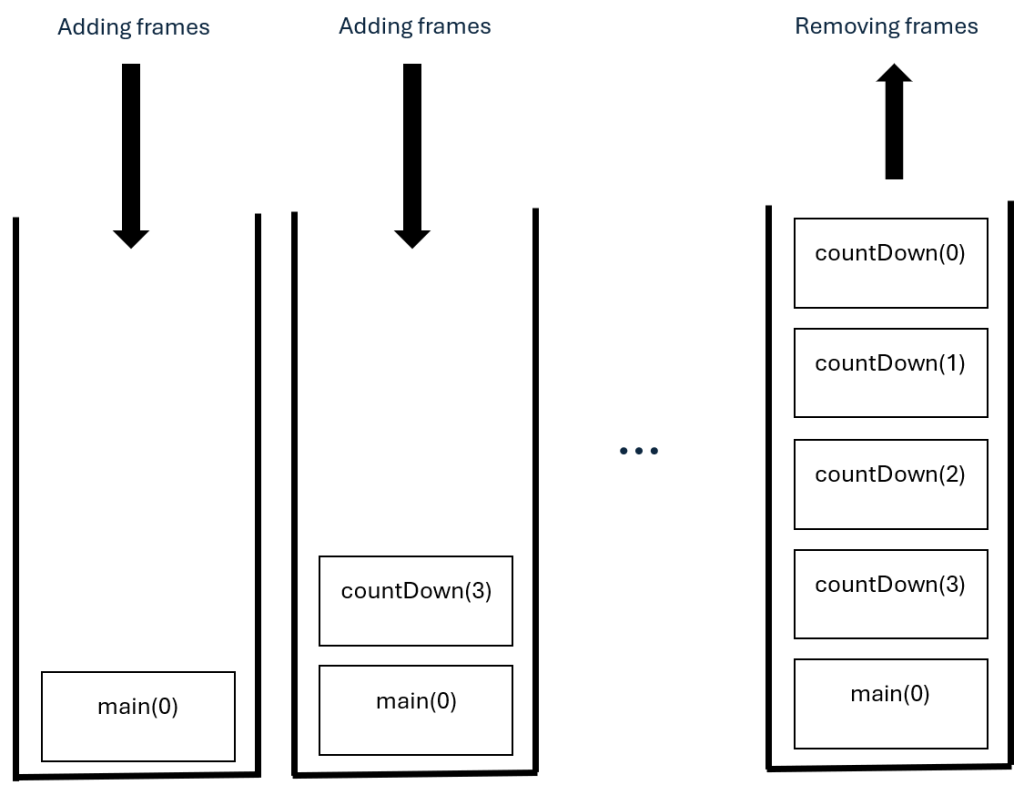
As you have already seen so far, recursion can create many copies of the recursive function. This can lead to a runtime error called a Stack Overflow, which occurs when all available memory for running a program is used up. But what are stacks? Stacks are a data structure used to organize data by controlling how data must be added and removed from the stack. Figure 02 shows what stacks look like. A stack can be thought of as a single-opening container, meaning there is only one opening for both adding and removing data. Each time a new recursive call is made, a new frame is added to the top of the stack. When the execution reaches the last recursive call, which is now at the top of the stack, that frame is removed, effectively freeing memory. This process continues until the first frame added to the stack is removed. Thus, stacks are known as Last-In, First-Out (LIFO) data structures.
Example 02
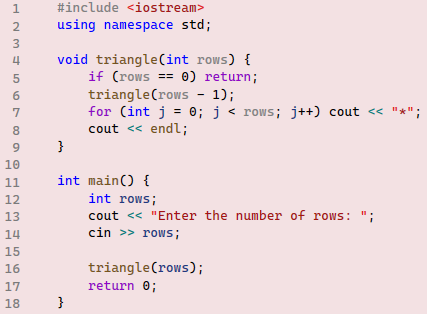 Run the given code and comment on the results. Figure 3 illustrates the execution flow. The program starts executing at the main() function, where the triangle(rows) recursive function is called for the first time on line 16. The execution control then moves to the first copy of the triangle(rows) function created in RAM. At this point, as the variable rows value is 3, the if-statement condition in the function returns false, causing the second recursive call to be invoked on line 6. Note that the remaining code in lines 7 and 8 will not be executed until the execution control returns to this particular copy of the triangle(rows) function. The execution control then moves to the second copy of the recursive function, where the argument rows is 2. The if-statement condition still returns false, and the third recursive call is invoked with an argument value of 1. In the final recursive call, the argument rows is 0, which causes the if-statement condition to return true, terminating this particular copy of the recursive function. The execution control then returns to the previous copy of the triangle(rows) function, resuming from where it left off—specifically, the for loop in line 7. As the for loop executes, the rows value is 1, so one star is printed to the console. When this function finishes execution and is terminated, the execution control returns to the previous recursive call, where the rows value is 2, and the for loop prints two stars. This process continues recursively, with the number of stars printed corresponding to the rows value. The execution control eventually returns to the main() function. If any code remains in the main() function, it will resume execution until the end of the main() function body, at which point the program terminates.
Run the given code and comment on the results. Figure 3 illustrates the execution flow. The program starts executing at the main() function, where the triangle(rows) recursive function is called for the first time on line 16. The execution control then moves to the first copy of the triangle(rows) function created in RAM. At this point, as the variable rows value is 3, the if-statement condition in the function returns false, causing the second recursive call to be invoked on line 6. Note that the remaining code in lines 7 and 8 will not be executed until the execution control returns to this particular copy of the triangle(rows) function. The execution control then moves to the second copy of the recursive function, where the argument rows is 2. The if-statement condition still returns false, and the third recursive call is invoked with an argument value of 1. In the final recursive call, the argument rows is 0, which causes the if-statement condition to return true, terminating this particular copy of the recursive function. The execution control then returns to the previous copy of the triangle(rows) function, resuming from where it left off—specifically, the for loop in line 7. As the for loop executes, the rows value is 1, so one star is printed to the console. When this function finishes execution and is terminated, the execution control returns to the previous recursive call, where the rows value is 2, and the for loop prints two stars. This process continues recursively, with the number of stars printed corresponding to the rows value. The execution control eventually returns to the main() function. If any code remains in the main() function, it will resume execution until the end of the main() function body, at which point the program terminates.

Exercise 01
Write a recursive function void printChars(char ch, int times) that prints the character passed as the ch argument a number of times equal to the value of the times argument. In the main function, ask the user to input the character they want printed and the number of times they want it printed.
Exercise 02
Modify example 02 to draw the triangle upside down. Explain how the change you made gets the desired output.
Exercise 03
Write the recursive function void printNumbers(int n, int& sum) that prints out numbers from 1 up to a positive number n, along with their sum. Sample run:
![]()
Recursive functions that return values
Recursive functions can be written to solve many problems. Therefore, recursive functions can either be void or return values of any type, such as int, double, string, etc. Writing void and non-void recursive functions is very similar. The only difference that we need to pay extra attention to is only the last returned value is usually the expected final value.
Example 03
The provided code contains a recursive function that calculates the factorial of any positive number. Line 12 demonstrates how calling a recursive function is similar to calling an iterative function. The string “The factorial of ” is first printed to the console, followed by the value stored in the variable num. Then, the string ” is: ” is printed, and the recursive function is called. At this point, execution control moves to the factorial function defined on line 4.
Figure 4 illustrates the execution flow. When the if-condition returns false, the recursive function is called again with the updated argument (n – 1). This pattern continues until the base case is reached, where the if-condition returns true, and the function returns the value 1 to the previous recursive call. At this point, the calculation can be completed and returned to the previous recursive call. This pattern continues until the first recursive call returns the final result to the main function.


Recursion is a powerful programming technique used to solve problems that can be broken down into smaller, similar subproblems. By calling the same function within itself, recursion allows for elegant solutions to complex problems. In Chapter 6, we discussed the binary search algorithm. Binary search works by repeatedly dividing the array into halves, thereby reducing the total size of the array. By continuing this process, the search problem is minimized to the smallest possible array, which contains only one item. This makes implementing the binary search algorithm recursively ideal.
Examples 04
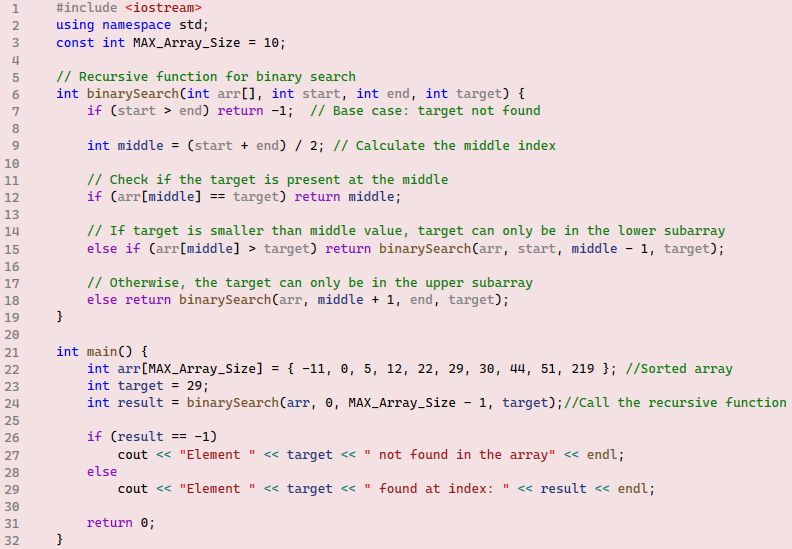
Figure 05 from Chapter 6 is presented again here for convenience.
The recursive binarySearch function takes four arguments: a sorted array, the starting and ending indices of the search range, and the target value to find. The initial search begins with a starting index of 0 and an ending index equal to the array’s size minus 1.
Each time binarySearch is called, line 7 checks if the starting index has exceeded the ending index. If this condition is true, it indicates that the entire search range has been examined without finding the target. In this case, line 7 returns -1, signaling that the target is not present. The main function then uses this return value to display an appropriate message to the console, as seen in lines 26 to 29. If the condition in line 7 is false, the search continues.
Line 9, calculate the middle index that will be used in the following if..else statement. Note that sometimes, the calculated middle index has a fraction. Of course, this is illegal and cannot be used as an index. Therefore, the middle variable is declared as an int, which discards any fraction (if any) in the middle variable value.
Line 12 compares the target value with the value stored in the middle index. In the provided example, the target is 29, and the middle index initially points to 22. Since these values are different, the else condition is evaluated. The function then makes a recursive call, either on line 15 or line 18, depending on whether the target is smaller or larger than the middle value. If the target is smaller, the search range is narrowed to the lower half of the array by adjusting the ending index. Conversely, if the target is larger, the search range is narrowed to the upper half by adjusting the starting index.
This process repeats with each recursive call, effectively halving the search range until either the target is found or the condition in line 7 becomes true, terminating the recursion.

Exercise 04
Write a program that reverses the user’s input. As we do not know the size of the input in advance, you must use a vector to store the input as characters using the cin.get() member function. Reversing the order of the characters is handled by the recursive function void reverseChars(vector<char>& chars, int start, int end). Reading the input and printing out the reversed input must be done in the main function.
Exercise 05
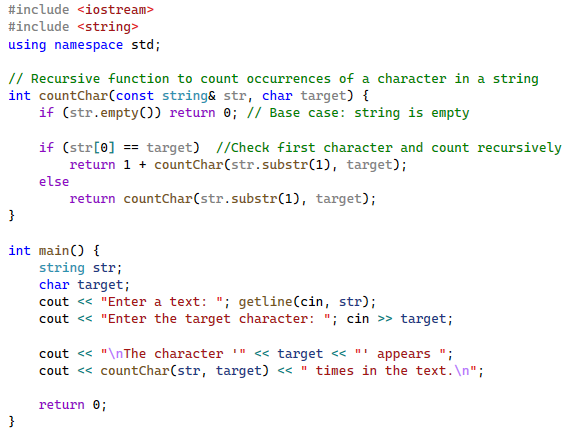
Write a program that counts how many times a character occurs in a given text. The program must have the recursive function int countChar(const string& str, char target) to achieve this task. The main function will get the text from the user and print out the result.
Hint: It is helpful to utilize the string class member functions like substr(), empty(), and others as needed.
Exercise 06
Write a program that calculates the length of a given string. The program must have the recursive function stringLength that takes a parameter of type string and returns an integer. The stringLength returns 0 if the string is empty.
Exercise 07
Determine the output for each of the following recursive functions for n = 4:
1)
int mountain(int n) {
if (n <= 1) return n * 2;
else return mountain(n - 1) + mountain(n - 2);
}
2)
int stream(int n) {
if (n == 0) return 3;
else return stream(n - 1) - n;
}
3)
int valley(int n) {
if (n <= 0) return 1;
else return valley(n - 1) * (n + 1);
}
Wrap up
This chapter introduces the concept of recursion in programming, where a function calls itself. It begins by comparing an iterative code with a recursive one, highlighting the need for a base case to prevent infinite loops in recursion. The chapter explains how recursive calls create new frames on the call stack, leading to potentially higher memory consumption compared to iteration and the risk of stack overflow. The Last-In, First-Out (LIFO) nature of the stack in managing recursive calls is also discussed. The chapter then provides examples of both void and value-returning recursive functions.
Answer Key
Exercise 01:

Exercise 02:
You only need to place the recursive call, triangle(rows – 1), after the for loop, that is, after printing the stars. In this case, the first recursive call prints a number of stars equal to the passed argument rows first, and then calls the triangle(rows – 1). The scored recursive call prints the number of stars equal to rows -1, and so on.
Exercise 03:

Exercise 04:

Exercise 05:
Exercise 06:

Exercise 07:
1)
mountain(4)=mountain(3)+mountain(2)mountain(3)=mountain(2)+mountain(1)mountain(2)=mountain(1)+mountain(0)mountain(1)= 1 * 2 = 2mountain(0)= 0 * 2 = 0mountain(2)= 2 + 0 = 2mountain(3)= 2 + 2 = 4mountain(4)= 4 + 2 = 6
Therefore, mountain(4) returns 6.
2)
stream(4)callsstream(3)and subtracts 4:stream(3) - 4stream(3)callsstream(2)and subtracts 3:stream(2) - 3stream(2)callsstream(1)and subtracts 2:stream(1) - 2stream(1)callsstream(0)and subtracts 1:stream(0) - 1stream(0)returns 3 (base case).
Now, let’s work our way back up:
stream(1)=stream(0)– 1 = 3 – 1 = 2stream(2)=stream(1)– 2 = 2 – 2 = 0stream(3)=stream(2)– 3 = 0 – 3 = -3stream(4)=stream(3)– 4 = -3 – 4 = -7
Therefore, stream(4) returns -7.
3)
valley(4)callsvalley(3)and multiplies the result by (4 + 1) = 5:valley(3) * 5valley(3)callsvalley(2)and multiplies the result by (3 + 1) = 4:valley(2) * 4valley(2)callsvalley(1)and multiplies the result by (2 + 1) = 3:valley(1) * 3valley(1)callsvalley(0)and multiplies the result by (1 + 1) = 2:valley(0) * 2valley(0)returns 1 (base case).
Now, let’s work our way back up:
valley(1)=valley(0)* 2 = 1 * 2 = 2valley(2)=valley(1)* 3 = 2 * 3 = 6valley(3)=valley(2)* 4 = 6 * 4 = 24valley(4)=valley(3)* 5 = 24 * 5 = 120
Therefore, valley(4) returns 120.
End of Chapter Exercises
Projects
Project 01: Recursive Number Guessing Game
Objective: To design and implement a number-guessing game in C++ that utilizes recursion to handle the core guessing logic. This project will test your understanding of recursive functions, including defining base cases and recursive steps, managing function parameters, and controlling program flow using recursion.
Requirements:
-
Game Setup:
- The program should randomly generate a secret integer within a defined range, like between 1 and 100. But the range can be anything else if you want.
- The program should welcome the player and inform him/her about the selected range of the secret number.
-
Recursive Guessing Function:
- You must implement a recursive function to handle the player’s guessing process. This function should:
- Take four parameters: the secret number, the lower bound of the possible range, the upper bound of the possible range, and the counter variable to count the number of player guesses.
- Prompt the player to enter their guess within the current bounds.
- Base Cases:
- If the player’s guess is outside the current lower and upper bounds, inform him/her of the invalid guess and make a recursive call to the same function, prompting for input again within the valid bounds.
- If the player’s guess is equal to the secret number, congratulate him/her and display the number of guesses it took. This will be one of the stopping conditions for the recursion.
- Recursive Steps:
- If the player’s guess is lower than the secret number, inform him/her it’s “Too low!” and make a recursive call to the same function. The lower bound for the next recursive call should be updated to be one greater than the player’s current guess.
- If the player’s guess is higher than the secret number, inform them it’s “Too high!” and make a recursive call to the same function. The upper bound for the next recursive call should be updated to be one less than the player’s current guess.
- You must implement a recursive function to handle the player’s guessing process. This function should:
-
Game Control in
mainFunction:- The
mainfunction should:- Seed the random number generator to ensure different secret numbers each time the program runs.
- Define the initial range for the secret number and generate the secret number.
- Welcome the player and start the guessing process by making the initial call to your recursive guessing function.
- After the player guesses correctly, ask if they want to play again by entering ‘y’ or ‘n’.
- Implement a loop that allows the player to play multiple rounds of the game if they choose to. For each new game, a new secret number should be generated, and the guess counter should be reset.
- Display a thank you message when the player decides to quit.
- The
Grading Criteria:
- Correct implementation of the recursive guessing function with appropriate base cases and recursive steps.
- Proper handling of the game setup in the
mainfunction, including random number generation and the play-again loop. - Accurate tracking and display of the number of guesses.
- Clear and user-friendly output and prompts.
- Adherence to the requirement of using recursion for the guessing logic.
This project will challenge you to apply the concept of recursion to solve a problem in a structured and interactive way. Good luck!
Sample Run:
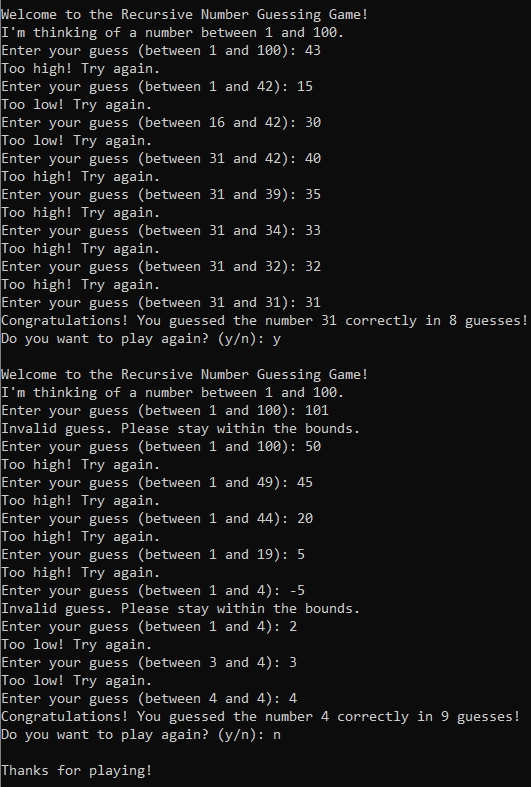
Project 02: Recursive Insertion Sort Implementation
The goal of this project is to help you understand and implement the recursive insertion sort algorithm. You will write a program that sorts an array of integers using a recursive approach and inserts elements into their correct positions.
Instructions:
1. Understand the Problem:
• You need to sort an array of integers using the recursive insertion sort algorithm.
• The algorithm will sort the array by recursively sorting the first n−1 elements and then inserting the last element into its correct position.
• You may search the web for tutorials if you need more details on how this algorithm works.
2. Write the Code:
• Create a function insertElement that inserts the last element into its correct position in a sorted subarray.
• Create a recursive function recursiveInsertionSort, that sorts the array by recursively sorting the first n−1 elements and then using insertElement to insert the last element.
• Write a main function to test your implementation with an example array.
3. Submission:
• Submit your source code file.
• Ensure your code is well-commented and follows good coding practices.
• Include a brief explanation of how your code works and any challenges you faced during implementation.
4. Evaluation Criteria:
• Correctness: The program correctly sorts the array using recursive insertion sort.
• Code Quality: The code is well-organized, readable, and follows good coding practices.
• Comments: The code is well-commented, explaining the logic and steps clearly.
• Explanation: The explanation of the code and challenges faced is clear and concise.
Tips:
• Test your code with different arrays to ensure it works correctly.
• Pay attention to the base case in the recursive function to avoid infinite recursion.
• Make sure to handle edge cases, such as an empty array or an array with one element.

