Place value and regrouping concepts are essential to understanding all mathematical operations. It is imperative these skills are learned with deep understanding and learned early. Our entire number system is based on the principle that “10 of something is the same as 1 of something else.” Learners must develop this concept, understand the principle of fair trade, and gain fluency in grouping and regrouping skills.

The vertical version of the Nudget is shown in this chapter. The vertical Nudget assists learners in connecting these concepts to the place value chart.

DEVELOPING PLACE VALUE CONCEPTS

1.  Have learners explore how to count and write numbers beyond 19.

2.  Ask learners to articulate what happens when they have to reset the Nudget.

3.  Guide learners in recognizing that each reset represents 10 checkers. Each reset count represents a set of 10 checkers.

4.  Introduce learners to the concept of “ten of something is equal to 1 of something else.” For example, 10 pennies is the same as 1 dime.

5.  Have learners use another Nudget to “count” each reset.

Count the number 26. Count, “I – 2 – 3 … 9.”

Count, “10.” Slide 1 checker to count 1 reset.

Reset.

Continue counting, “11, 12, 13 … 19”

Count, “20.” Slide 1 checker to count another reset.

Continue counting, “21, 22, 23 …. 26”

Counting 26, results in 2 resets and 6 checkers.

Learners should understand that each “reset” represents trading 10 for 1 of the next place value. It is helpful to use base 10 blocks in conjunction with developing place value concepts to develop the understanding of equal trading with 10.

DEVELOPING GROUPING CONCEPTS

1. Have learners count a two-digit number with the Nudget.
2. Introduce the concept of “grouping” when they have to reset the Nudget.
3. Learners should understand that by resetting the checkers, they are “grouping” and counting them as 1 set on another Nudget.
4. Guide learners in labeling the place values, “ones” and “tens.”

Count the number 43. Count, “I – 2 – 3 … 10.”

T          O

Count, “1I – 12 – 13 … 20.”

T          O

Count, “2I – 22 – 23 … 30.”

T          O

Count, “3I – 32 – 33 … 40.”

T          O

Count, “4I – 42 – 43.”

T          O

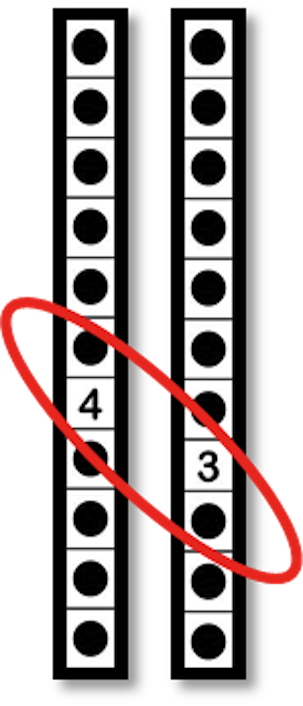Learners should understand that each reset on the ones Nudget represents grouping a 10 and counting 1 on the tens Nudget. Have learners explore counting two-digit, three-digit, and four- digit numbers to ensure this concept is fully developed. Guide learners in labeling “hundreds” and “thousands.”

DEVELOPING REGROUPING CONCEPTS

1. Have learners count a two-digit number with the Nudgets.
2. Ask learners to predict what will happen if they count backwards.
3. Guide learners in recognizing that they will have to trade in a ten to “reset” the Nudget and gain more checkers to continue the counting.
4. Introduce the concept of “regrouping” to trade 1 for 10 of a smaller place value.

Start with the number 43.

Count backwards, “43 – 42 – 41 – 40.” Regroup.

Count, “39 – 38 – 37…30.” Regroup.

Count, “29 – 28 – 27…20.” Regroup.

Count, “19 – 18 – 17…10.” Regroup.

Count, “9 – 8 – 7…0”

Learners should discover that when counting backwards each “reset” represents trading 1 ten for 10 checkers to continue the count. It is important learners fully understanding trading up and trading down with place values. Have learners explore counting back two-digit, three-digit, and four- digit numbers to ensure this concept is fully developed.

ADDITION WITH REGROUPING

1. Have learners show a one-digit number.
2. Ask learners to count on another one-digit number.
3. Give learners a number that requires regrouping.

Start with the number 8.

Count on 7 more. Count, “1.”

Count, “2.”

Group and reset.

Count, “3.”

Count, “4 – 5 – 6 – 7.”

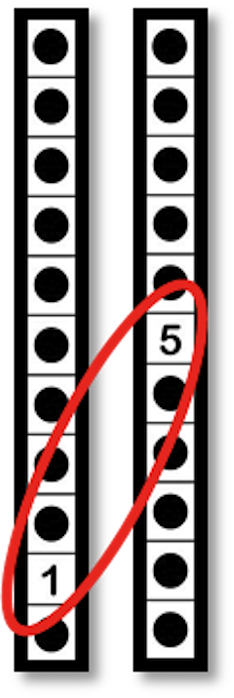Write:   8 + 7 = 15

Learners should understand that each “reset” represents trading 10 for 1 of the next place value. Use the vertical Nudgets when possible to assist learners in connecting to abstract notation. Guide learners in discovering why to “carry the 1” as in the traditional algorithm. Have learners explore adding one-digit to one-digit, two-digit to one-digit, and two-digit to two-digit numbers to ensure this concept is fully developed.

SUBTRACTION WITH REGROUPING

1. Have learners show a two-digit number.
2. Ask learners to count back a one-digit number.
3. Give learners a number that requires regrouping.

Start with the number 15.

Count back 9 checkers. Count, “1 – 2 – 3 – 4 – 5.”

Regroup.

Continue counting back, “6 – 7 – 8 – 9.”

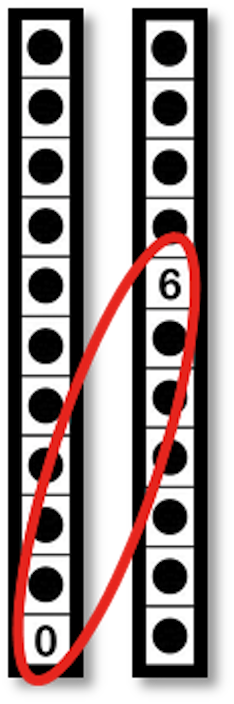Write:   15 – 9 = 6

Learners should understand that each “reset” represents trading 1 for 10 of the next lower place value. Use the vertical Nudgets when possible to assist learners in connecting to abstract notation. Guide learners in discovering when they need to “borrow a 1” as in the traditional algorithm. Have learners explore subtracting one-digit from two-digit, and two-digit from three-digit numbers to ensure this concept is fully developed.