7 Whole Number Place Value

The focus of chapter 6 was on number sense and a relational understanding of numbers. Number sense is linked to place value and an understanding of the base-ten number system. The progression of place value across grades K-5 is critical for understanding:

1. Decomposing numbers in base ten
2. Reading and writing numbers
3. Rounding numbers
4. Comparing numbers and quantities in base ten.

By the end of kindergarten, students are expected to count to 100 and count sets of 20 (KSDE, 2017a). In kindergarten, counting is based on a ones approach – the number 15 means 15 ones. According to Wright, et. al. (2006), there is a progression to understanding ten:

1. children understand ten as ten ones,
2. children see ten as a unit, and
3. children easily work with units of ten.

Consider the phrase, “ten ones make one ten.” And now think like a child. How does this make sense? Students in phase one count a set of items and think of that set as ones. When students move to phase two, they begin to see a group of ten as a unit, such as a group of ten ones.

We use the base-ten system; using ten digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Every number can be represented using these digits. In the base-ten system, the value of each place is always 10 times the value of the place to the immediate right. When moving one place left, the value of the place is multiplied by 10.

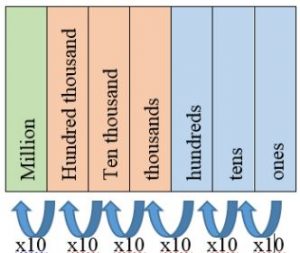
In the base-ten system, the “places” are ones, tens, hundreds, thousands, etc. And the digit in each place represents 0-9 of those units. Students learn that ten ones makes a unit, called a ten. They then learn that two-digit numbers are composed of ones and tens.

Place value is a fundamental concept in the elementary grades, and understanding place value is essential in learning mathematics. Place value is the value of the digit in its position. For example, the number 358 has three columns or “places,” each with a specific value. In 358,  the 3 is in the “hundreds” place, the 5 is in the “tens” place, and the 8 is in the “ones” place. But more importantly, the value of each digit is 3 hundreds (or 300), 5 tens (or 50), and 8 ones.

Base-Ten Blocks

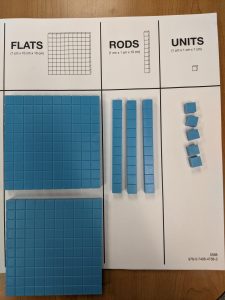
Base-ten blocks provide a hands-on model of our base-ten number system. The smallest cubes are called units. The long, narrow blocks are called rods. The flat, square blocks are called flats. The large cubes are called cubes. The size relationships of the base-ten blocks are perfectly designed to help children discover that it takes 10 units to make one rod, or 10 ones to make one ten; and 10 tens to make one hundred.

Base-ten blocks are ideal for students to physically manipulate “the numbers” so they can conceptually understand the concepts of place value. Nothing can replace the physical manipulatives used to help students make the connections from concrete to abstract understanding.

An example showing the relationship among the manipulatives, the place or position, and the place value of the digits in a number is below.

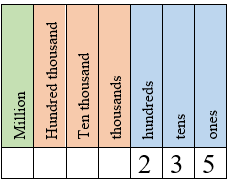
The number 235 is written in standard notation. This shows the “value” of each digit. There are two hundreds, three tens, and five ones. Additionally, in the number 235: 2 is in hundreds place and its place value is 200, 3 is in tens place and its place value is 30, 5 is in ones place and its place value is 5.

Understanding the place value of digits in numbers helps in writing numbers in their expanded form. For instance, the expanded notation of the number 235 is 200 + 30 + 5.

According to James Brickwedde (2012), “place value and the base ten system is an early and easy entry point for students to begin to explore this agility. Without this level of flexibility and fluency, students are limited to inefficient strategies or are overly dependent upon tactical procedures they know only through rote application.”

Your language matters when teaching students about place value. Speak in value, not in digits. For example, the value of the 2 in 26 is two tens or 20.

Kindergarten

Kindergarten is the first time many students work with numbers greater than 10 using manipulatives and/or drawings. Kindergarten students separate (decompose) a set of 11-19 objects into a group of 10 and some other ones. Experiences with double ten frames will help students to understand this concept.

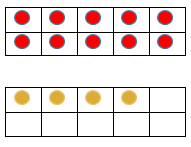
Notice the grouping of the ten. It is obvious that there is one group of ten with some others left over. Students will immediately see that 14 is made up of one ten and four ones.

The “teen” numbers are one group of ten and some more ones. Notice the “teen” numbers that do not follow a particular pattern in the counting sequence. First, think of the number names 11-19: eleven, twelve, thirteen, fourteen, fifteen, sixteen, seventeen, eighteen, nineteen.

• Eleven and twelve are special number words that do not have “teen” as a suffix.
• The verbal counting of “teen” numbers is backwards: the ones digit is said before the tens digit. For example, 37 is read as thirty-seven; tens to ones. But the number 14 is read as fourteen; read ones to tens.

When teaching the “teen” numbers, ask students to read the number as well as describe the quantity. For the number 18, students should read “eighteen” and then say, “18 is one group of ten and eight ones.” Additionally, students should record the number sentence 18 = 10 + 8.

By the end of kindergarten, students should be able to compose and decompose numbers between 11 and 19 into tens and some ones. When teaching to compose and decompose numbers, students must use manipulatives and drawings.

Source: KSDE Flip Book Kindergarten (2017b)

Check out the task “What Makes a Teen Number?” at the Illustrative Mathematics website. This activity helps students decompose teen numbers using ten-frames and number sentences.

First Grade

In the first grade Domain Number and Operations in Base Ten, the second Cluster is understand place value. Thinking about “10 ones makes 1 ten” is confusing for students. In first grade, students should see 10 ones as 1 ten and that 1 ten has the same value as 10 ones.

Students need many opportunities to practice grouping 10 ones into a bundle of 10. In first grade, students begin to unitize. They see that a group of ten objects is also one ten.

Watch this video “One Is One, Or Is It?” narrated by Christopher Danielson for more information on unitizing.

Students must be given numerous experiences using ten-frames, snap cubes, or other groupable models to help develop the concept of place value.

Suggested Activity using Ten-Frames:

Give students 13 counters.

Teacher: “Do you have enough to make a ten?” “Would you have any left over?” “If so, how many left overs do you have?”

Student: “I have filled up one ten-frame and have 3 counters left over. The number 13 has 1 ten and 3 ones.

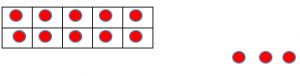
In first grade, students explore the decade numbers (10, 20, 30, 40, 50, 60, 70, 80, 90) as groups of ten with no ones left over. Students use manipulatives to group, or bundle, groups of ten. As students count any number up to 99, they should group/bundle tens and some more. Furthermore, they should focus on the mathematical language associated with the quantity. For example, the number 62 can be expressed as 62 ones; or 6 groups of ten with 2 left over.

In addition, students should read numbers in standard form AND using place value concepts. Read the number 62 as “sixty-two” as well as 6 tens and 2 ones.

First grade students “compare two two-digit numbers based on meanings of the tens and ones digits, recording the results of comparisons with the relational symbols >, <, =, and ≠”. According to Dougherty, Flores, Louis, & Sophian (2010), students should determine whether quantities are equal or not equal before using “greater than” and “less than.” Once students know the two quantities are not equal, then teachers can have a discussion about “how” they are not equal by asking the following questions. “Which one is greater?” “Which one is less?” These discussions must occur before using the greater than and less than symbols.

Give students extensive experiences to explain their thinking using words and models before using the symbols. Students can use manipulatives to model the two numbers, as well as pictures or number lines. Again, it is critical that students develop the concept of composing and decomposing tens and ones. This is foundational to understanding place value and involves number relationships and promotes a flexibility with mental computation. Furthermore, students must learn through a progression of representations. They begin with concrete models, then move to pictorial models, and then abstract models.

Second Grade

In second grade, students work on decomposing numbers by using place value. Give students extensive experiences with manipulatives as well as pictorial representations of numbers. Students also should be able to decompose numbers into hundred, tens, and ones in several different combinations. For example, 268 could be shown as 2 hundreds, 6 tens, and 8 ones. But is also correct to show 268 as 26 tens and 8 ones, OR 1 hundred, 16 tens, and 8 ones. There are several ways to represent the number 268:

Building on their work in first grade, second grade students need multiple opportunities to count and bundle groups of hundreds. It is critical that students understand that 100 is 10 tens as well as 100 ones.

Students in second grade also  learn to read, write, and represent a number of objects in various forms

• Base-ten numerals – 268
• Number names – two hundred sixty-eight
• Expanded notation – 200 + 60 + 8
• Unit form – 2 hundreds, 6 tens, 8 ones

Notice, in the number names, the word “and” is not used between any of the whole number words. Save the word “and” for decimals.

Second grade students build on their work in first grade to compare two numbers and use the relational symbols of <, >, =, and ≠. Give students extensive experiences to explain their thinking using words and models before using the symbols. Students can use manipulatives to model the two numbers, as well as pictures or number lines.

Another way to ensure that students develop a conceptual understanding of the relational symbols (<, >, =, and ≠), use a number line. Be sure to put the greater than and less than symbols above the number line.

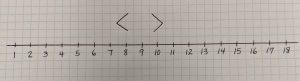
Then share the two numbers you want to compare; for example 14 and 7. Explain to students that you want to compare where 14 is in relation to the number 7. So you can move the two relational symbols above the 7.

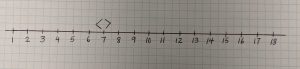
Ask students where 14 is in relation to 7. Is it to the left, which would be lesser number? Or is it to the right, which would be greater number?

Using relationships truly focuses on the numbers and on tricks.

Additionally, second grade students fluently add using strategies based on place value. For example, using the place value strategy for 56 + 27, a student might say:

• I decomposed 56 and 27 into tens and ones.
• 5 tens plus 2 tens is 7 tens.
• Then I added the ones; 6 ones and 7 ones is 13 ones.
• Then I combined the tens and ones. 7 tens plus 13 ones is 83.

Source: 2017 Kansas Mathematics Standards Flip Book 2nd Grade

Rounding Whole Numbers

The first time students encounter rounding whole numbers is in third grade. Students “use place value understanding to round whole numbers to the nearest 10 or 100.” Additionally, students should have a deep understanding of place value and number sense in order to explain and reason about their rounded answers.

When teaching students about rounding, you are deciding which number is closest. For example, 127 is closer to 100 than it is 200. If students don’t know this, then there is a gap in their place value understanding.

A strong understanding of place value is critical for students to understand rounding of whole numbers. Don’t begin by telling students the rules; use a number line so that students can develop a conceptual understanding of rounding. Students need to learn when and why to round numbers by first identifying possible answers and the halfway point.

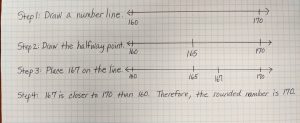
Using an open number line to teach students about rounding will help both their rounding skills and strengthen place value understanding. For example, round 167 to the nearest ten.

Source: KSDE Flip Book 3rd Grade (2017c)

Teaching Greater Than and Less Than

Don’t teach greater than and less than using methods such as “Pac Man” or “Alligator” or other aids. When you use these, students don’t grasp the full meaning of the relational symbol. If you must use one of these “learning aids,” be sure to include the mathematical name and symbol with it. But first, explicitly teach that the symbols have names. Second, ask students to read the entire inequality, reading the numbers and symbols left to right, in the same way they would read a sentence.

For example, when students write 5 < 8, they would read this sentence as “five is less than eight.” This is a critical step in learning these relational symbols. Additionally, when students read the inequality aloud, they can recognize errors. For example, 5 < 8, if students say five is greater than eight, that does not make sense and they can correct their mistake.

Calculators in the Elementary Mathematics Classroom

The NCTM (2015) Position Statement, “Calculator Use in Elementary Grades,” states:

Calculators in the elementary grades serve as aids in advancing student understanding without replacing the need for other calculation methods. Calculator use can promote the higher-order thinking and reasoning needed for problem solving in our information- and technology-based society. Their use can also assist teachers and students in increasing student understanding of and fluency with arithmetic operations, algorithms, and numerical relationships and enhancing student motivation. Strategic calculator use can aid students in recognizing and extending numeric, algebraic, and geometric patterns and relationships.

Calculators in the elementary classroom are essential in helping students make sense of mathematics and reason mathematically. Teachers need to plan for the strategic use of calculators that will support student thinking and assist them in making connections to real-world situations.

Read NCTM’s Position Statement “Calculator Use in Elementary Grades.”