8 Whole Number Computation

Computational fluency is the ability to accurately, efficiently, and flexibly compute with basic operations (National Research Council, 2001) and is developed over time. In elementary school, students learn about the four basic operations, the properties of the operations, and the strategies to perform those operations. It is developed progressing from concrete models to drawings and then to symbols. The Concrete Representational Abstract (CRA) approach  helps students make the connection from concrete manipulatives to abstract mathematical ideas. The three stages of learning mathematics are:

• Concrete – students physically manipulate objects to solve a mathematics problem

• Representational (or semi-concrete) – involves using images to represent objects.
• Abstract (or symbolic) – using only numbers and symbols to solve math problems.

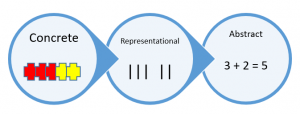
CRA is grounded in the constructivist theory of learning. Teachers begin with concrete manipulatives, transition to visual representations/drawings, and then move to abstract mathematical numbers and symbols. When teaching students addition and subtraction, begin with models/manipulatives, and then progress to bar diagrams, and number lines.

Watch the video from Graham Fletcher, “The Progression of Addition and Subtraction.”

Addition and Subtraction Computation

In kindergarten, students developed an understanding of addition as putting together and adding to, and subtraction as taking apart and taking from. Students in first grade are expected to add two-digit numbers to one-digit numbers; and in second grade, students add two- and three-digit numbers. It is important to note that the traditional algorithms are not required until fourth grade. Therefore, students are expected to compose and decompose numbers and use flexible methods to solve problems.

When adding two or more numbers, the result is the sum. The symbol used for addition is the plus sign (+). The inverse of addition is subtraction, and the result is called the difference. The symbol used for subtraction is the minus sign (-).

First grade students will extend their number facts and place value strategies to add within 100.  Do not introduce the traditional addition or subtraction algorithms in first grade. Instead, represent a problem using words, numbers, pictures, manipulatives, and/or symbols.

Using Base Ten Blocks to Add and Subtract

Base Ten Blocks provide a concrete model of our base ten number system. Base-ten blocks provide a hands-on model of our base-ten number system. The smallest cubes are called units. The long, narrow blocks are called rods. The flat, square blocks are called flats. The large cubes are called cubes. The size relationships of the base-ten blocks are perfectly designed to help children discover that it takes 10 units to make one rod, or 10 ones to make one ten; 10 tens to make one hundred; and 10 hundreds to make one thousand.

Base-ten blocks are ideal for students to physically manipulate “the numbers” so they can conceptually understand the concepts of place value.

Examples:

Addition Example: 53 + 38 =

• Students begin by placing 53 base-ten blocks (5 rods and 3 units) and 38 base-ten blocks (3 rods and 8 units) on their table.
• Students will then combine groups of ten ones and trade that group for 1 ten/rod.

Subtraction Example: 135 – 48 =

• Students begin by placing 135 base-ten blocks on their table.
• Students will then remove 48 from this set of base-ten blocks. Students will notice immediately that they can not remove eight ones/units because there are only 5 on the table. Therefore, they will need to regroup/exchange/trade one ten/rod for ten ones/units so they can take away 8 ones.
• Then regroup/exchange/trade the one hundred/flat for ten tens/rods.

Addition and Subtraction Based on the Properties of Operations

In first grade, students applied the properties of operations to add and subtract. They can then build on these understandings to fluently add and subtract using the properties, such as the Commutative Property of Addition and the Associative Property of Addition.

Addition Example: 37 + 25

• I decomposed the 37 and 25 into tens and ones so now I have 30 + 7 + 20 + 5.
• I add 30 and 20 first to get 50.
• Then I add 7 and 5 to get 12.
• Then 50 + 12 is 62.

Addition and Subtraction with Bar Diagrams

Another model to use when adding and subtraction is the bar diagram. Bar diagrams (sometimes called strip or tape diagrams) are a pictorial representation of a problem shown by bars or boxes. Using bar diagrams is the representational/semi-concrete link between the concrete and the abstract phases of learning..

Note the following examples:

Susan made 24 cookies for the school carnival. Terry made 36 cookies. How many cookies will the school carnival have to share?

Kathryn has read 17 books. Her goal is to read 52 this year. How many more books does she need to read?

Addition and Subtraction with Open Number Lines

An open number line has no numbers or marks on it; it is used when students want to share their thinking strategies. Before using the open number line, students must have a strong understanding of numbers up to 100. Prerequisite skills include counting on and counting back, knowing basic addition and subtraction facts to ten, and adding/subtracting a multiple of 10 to or from any two-digit number.

To introduce the open number line, ask students questions such as:

• How can you go from 0 to 37 in the least number of jumps of tens and ones?

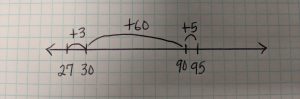
Encourage students to share their strategies and discuss which strategy is most efficient. For example, when jumping from 0 to 37, one student could say, “three jumps of ten and seven jumps of one” and another student could say, “four jumps of ten and back three ones.”

When students have mastered questions like the one above, the next phase in the use of the open number line is with addition and subtraction. Be sure to give students the flexibility to choose what types of jumps they want to use. Some possible questions are:

• How can you go from 26 to 52 in a small number of jumps? Who has another strategy?

• How can you go from 61 to 37 in a small number of jumps? Who has another strategy?

• How can you solve 27 + 85?
• How can you solve 68 – 31?

To solve the problem 27 + 68, one student may begin at 27, add 60 and then add 8.

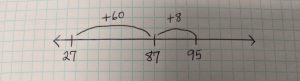
Another student may solve 27 + 68 by adding 3, then add 60, then add 5.

Multiplication and Division Computation

Second grade students will “use addition to find the total number of objects arranged in rectangular arrays” (KSDE, 2017). Rectangular arrays are an arrangement of objects in horizontal rows and vertical columns and provides a visual model for multiplication. One way to introduce students to arrays is to ask them to build all possible arrays with no more than 25 objects, and up to 5 rows and 5 columns (5 x 5 array). In addition, ask students to draw their arrays on grid paper and write two different equations under their array. An example of this is a 5 x 4 array:

• The equation by rows is 20 = 5 + 5 + 5 + 5
• The equation by columns is 20 = 4 + 4 + 4 + 4 + 4

Source: 2017 Kansas Mathematics Standards Flip Book 2nd Grade

Students must explore the concept of rectangular arrays using concrete objects, as well as pictorial representations on grid paper. In addition, students will use the commutative property of addition since they can add either the rows or columns and get the same answer.

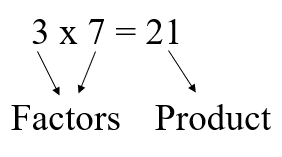
In third grade, students will find the products of whole numbers and recognize multiplication as finding the total number of objects when there are an equal number of groups. Refer to “groups of” objects, such as 4 x 7 is 4 groups of 7. Begin using the vocabulary terms factor and product at this level.

Be sure to refer to Table 2 in the Kansas Mathematics Standards for the types of multiplication problems.

Students must experience all three types of multiplication problems: size of group is unknown, unknown product, and number of groups is unknown. When students are solving problems, ask them to also write the related multiplication or division equation. For example, to determine the unknown number in the equation 24 ? = 3, students should use their knowledge of the related multiplication fact 3 x 8 = 24.

Watch this video from Graham Fletcher, “The Progression of Multiplication”

When teaching division, focus on two models of division: partitive and measurement.

• Partitive division focuses on the question, “How many are in each group?” An example of the partition model in context is, “There are 15 cookies on the counter. If you are sharing the cookies equally among 5 friends, how many cookies will each friend receive?”
• Measurement division (sometimes called repeated subtraction) focuses on the question, “How many groups can you make?” An example of the measurement model is, “There are 15 cookies on the counter. If I give each person 3 cookies, how many people can I give cookies to?”

In third grade, students should be introduced to the vocabulary terms for division: quotient, dividend, and divisor. In addition, students should use models and concrete objects to justify their thinking.

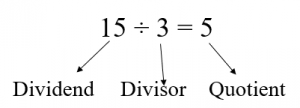
In third grade, students use various strategies to solve word problems. Expect students to use a variety of representations when solving problems, such as rectangular arrays, drawing pictures of equal groups, mental math, number lines, and equations.

Watch this video from Graham Fletcher, “The Progression of Division.”

Examples of Multiple Strategies for Teaching Multiplication in Third Grade:

There are 24 books to be displayed on the library shelves. If the books are displayed with 4 books on each shelf, how many shelves would be needed?

Rectangular Array

Mental Mathematics

A student could reason that “6 and 6 are 12” and “12 and 12 are 24.” Therefore, there are 4 groups of 6 for a total of 24 books.

Number Line

A number line can show the jumps of equal distance.

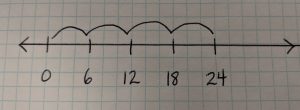
Equations

Students may use related equations, such as

• 4 x 6 = ?
• 6 x 4 = ?
• 24 × ? = 4
• 24 ÷ 6 = ?
• ? ÷ 4 = 24
• ? ÷ 6 = 4

Furthermore, third graders should be introduced to variables. Letters for variables should begin being used in third grade for the unknown number, for example, 24 ÷ x = 4.

When students use various strategies and multiple representations, you are helping them develop multiplicative reasoning. Multiplicative reasoning is the ability to work flexibly with the concepts, strategies and representations of multiplication (and division). It helps students see the different kinds of relationships between numbers, whereas additive thinking only requires a capacity to work with the numbers themselves (Siemon, 2015). Multiplicative reasoning is related to iterating, or making multiple copies.

Examples of Multiple Strategies for Teaching Division in Third Grade:

The two strategies students can use to solve division word problems are using diagrams and/or pictures (partitive division) or determining the number of shares (measurement division).

This is an example of partitive division since the size of the groups is unknown. Shelby has 36 candies to share equally with her 4 friends. How many candies will each person receive?

This is an example of measurement division since the number of groups is unknown. Amie loves sodas and buys one every afternoon. Each soda costs $2. If she has $12, how many days can she buy a soda?

Therefore, it took 6 days for Amie to spend her $12 on sodas.

Properties of Multiplication

Students in third grade are expected to understand the properties of multiplication, although they do not need to use the formal terms. Teachers must use the correct terms.

The four mathematical properties of multiplication that students need to be familiar with and use:

• Commutative Property of Multiplication,
• Associative Property of Multiplication,
• Multiplicative Identity Property, and
• Distributive Property of Multiplication over Addition.

The Commutative Property of Multiplication is when two numbers are multiplied, the product is the same regardless of the order of the factors. To “commute” means to travel, and according to the Commutative Property of Multiplication, the numbers can “move around” without changing the product. For example, the array 3 x 4 can also be shown as the array 4 x 3.

The Associative Property of Multiplication is when three or more numbers are multiplied, the product is the same regardless of the grouping of the factors. “To associate” means to connect or join with something; and according to the Associative Property of Multiplication, numbers can “associate” with any other number. For example, 6 x 5 x 2 could be solved the following ways:

(6 x 5) x 2

• Multiply 6 x 5 first = 30

OR 6 x (5 x 2)

• Multiply 5 x 2 first = 10
• Then 30 x 2 = 60 Then 6 x 10 is 60.

The Distributive Property of Multiplication over Addition is when multiplying a sum by a number is the same as multiplying each addend separately and then adding the products. To “distribute” means to spread out equally. For example, 8 x 7 could be shown in a rectangular array and then decompose 7 into 5 and 2.

Source: Kansas Mathematics Standards Flip Book 3rd grade (2017a)

Fact Triangles

Fact Triangles can be used to help students see the inverse relationships between multiplication and division.

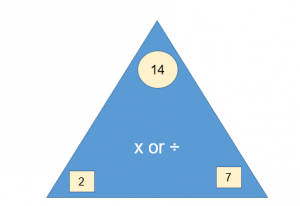
2 x 7 = 14              7 x 2 = 14

14 ÷ 2 = 7             14 ÷ 7 = 2

2 = 14 ÷ 7              7 = 14 ÷ 2

Click here for Fact Triangles printables.]

By the end of third grade, students will fluently multiply and divide single digit numbers within 100. This does not mean a focus on timed tests, but focus on hands-on experiences, working with manipulatives and drawing pictures. In addition, give students multiple opportunities to experience multiplication and division problems written both horizontally and vertically. Refer to chapter 5 for strategies students can use to develop fluency with basic multiplication and division facts.

Estimation

Don’t teach estimation by asking students “make a guess.” The word “estimate” comes from the Latin word aestimare, which means to value. To estimate means to judge the value of something, and an estimate is the resulting calculation. A “guess” is to form an opinion with little or no evidence. When you tell students to make a guess, they are making uninformed conclusions. On the other hand, estimating means to make an informed decision based on data and models (Nichol, n.d.).

Teaching Traditional Algorithms

Traditional algorithms are digit oriented whereas invented strategies are number oriented. When students invent strategies for solving problems, they are more flexible with the problems. With the traditional algorithm, students see and do the problem following rules. Additionally, with invented strategies, students make fewer errors.

The Kansas Mathematics Standards suggest that students have knowledge of standard/traditional algorithms in fourth grade for addition and subtraction, fifth grade for multiplication, and sixth grade for division. These topics are introduced much earlier than the grade level for the standard algorithm so that students can make sense of why that algorithm works. The key is that students understand the mathematical operations before they learn the “rules” of traditional algorithms.