11 Algebraic Thinking

What is algebraic thinking?
As you read the Kansas Mathematics Standards, you will notice the Domain “Operations and Algebraic Thinking” in all grade levels preK grade 12. Furthermore, algebraic thinking and concepts permeate all areas of mathematics. Algebra is more than manipulating symbols or a set of rules, it is a way of thinking.
According to the K-5 Progression on Counting & Cardinality and Operations & Algebraic Thinking (2011), algebraic thinking begins with early counting and telling how many in a group of objects, and builds to addition, subtraction, multiplication, and division. Operations and Algebraic Thinking is about generalizing arithmetic and representing patterns.
Algebraic thinking includes the ability to recognize patterns, represent relationships, make generalizations, and analyze how things change. In the early grades, students notice, describe, and extend patterns; and they generalize about those patterns. Elementary students use patterns in arrays, and they look at patterns to learn basic facts. According to NCTM Past-President Cathy Seeley, “the development of algebraic thinking is a process, not an event. It is something that can be part of a positive, motivating, enriching school mathematics experience” (Seeley, 2004).
Algebra must be incorporated into the elementary classroom as students see patterns, make generalizations, and move across representations. It is essential that algebra instruction focus on sense making, not symbol manipulation (Battista & Brown, 1998). According to Earnest and Balti, “When elementary teachers are unfamiliar with early algebra, lessons designed and labeled as algebraic may become arithmetic exercises; the algebra then remains hidden from both the teacher and students in the implementation. The result is that the algebra standard is only superficially addressed” (Earnest & Balti, 2008).
Blanton and Kaput (2003) suggest teachers “algebrafy” their current curriculum materials and ask students to discover patterns and make conjectures and generalizations, and justify their answers. They also recommend that teachers use these prompts to extend students’ thinking:
- Tell me what you were thinking.
- Did you solve this in a different way?
- How do you know this is true?
- Does this always work?
Therefore, all elementary teachers must support algebraic thinking and create a classroom culture that values “students modeling, exploring, arguing, predicting, conjecturing, and testing their ideas, as well as practicing computational skills” (Blanton & Kaput, 2003).
Key ideas that underscore algebraic thinking are:
- Equality and the concept of equivalence
- Students often have the misconception that the equal sign means “the answer is” when it really means “the same as.” True/false equations are a way to expose students to the meaning of equality, such as 5 + 2 = 3 + 4, or 8 = 2 + 6.
- Inequality
- Develop in your students a conceptual understanding of greater than and less than as relational symbols, and not rely on memory tricks.
- Positive and negative numbers
- Students should be exposed to some negative numbers in the early grades. When teachers say, “You can’t take 6 from 3,” or “You can’t subtract a small number minus a big number,” teachers are giving students information that just isn’t true.
- Problem solving and critical thinking
- Students who have problem solving and critical thinking skills can solve problems in new contexts and can generalize to new situations.
- Making generalizations
- It is important that students discover patterns, which includes mathematical rules, in order to make conjectures about the growing pattern.
- Patterns
- “We need to train children to look for, and to expect to find, patterns in all math work that they do” (Bahr, 2008).
- Variables
- Variables are unknown and can change and are represented by symbols. Teachers should explicitly explain to students that the one-letter symbol is an abbreviation (Bahr, 2008).
- Relational thinking
- Relational thinking focuses on the why behind the right answer. For example, 5 x 3 = 15, but why? It is because there are three groups and each group has five.
- Symbolic representation of mathematical ideas
- Learning that equations communicate the relationship between numbers is crucial for a conceptual understanding behind the symbols.
Source: Algebraic Thinking (de Garcia, 2008)

Connecting Number and Operations and Algebraic Thinking
In kindergarten through grade 3, all of the Operation and Algebraic Thinking standards are related to Number and Operations in Base Ten.
Kindergarten
Students in kindergarten solve addition and subtraction problems in various ways as they make sense of and understand the concepts of addition and subtraction. Kindergarten students should see addition and subtraction equations, and should be encouraged to write equations, such as 4 + 3 = 7 and 7 – 3 = 4, but do not require this of students at this level. It is critical that students see the relationship between numbers, and teachers need to provide students those experiences to manipulate numbers using objects, drawings, mental images, etc. so that students can progress from the concrete, to the pictorial, to the abstract levels.
Kindergarten students work with numbers through 10 as they solve word problems. Be sure to focus on these three problem types: Result Unknown, Change Unknown, and Start Unknown. See Chapter 4 for more information regarding these types of problems as well as Table 1 in the Appendix of the Kansas Mathematics Standards.
Beginning in kindergarten, students should also see the equal sign as a relational symbol, not as an action to find the answer. Help students see the relationship between both sides of an equation as having the same value.
First Grade
All of the first grade standards under the Domain of Operations and Algebraic Thinking were addressed in Chapter 4 as students represent and solve addition and subtraction problems, apply the properties of operations and see the relationship between addition and subtraction, and add and subtract within 20.
Some students misunderstand the meaning of the equal sign, and it is critical to correct this misconception early. The equal sign is a relational symbol meaning “the same as.” The equal sign is not an operations symbol. Many children believe the equal sign means “the answer is,” which is incorrect. Consider the problem 3 + 7 = 9 + 1. There is no answer, although the two sides are the same. Also give students problems where the equal sign is at the beginning of the problem, for example, 8 = 3 + 5.
The Operations and Algebraic Thinking tasks in the Illustrative Mathematics website is a good resource for connecting number sense to algebraic thinking.
Second Grade
All of the second grade standards under the Domain of Operations and Algebraic Thinking were addressed in Chapters 4, 5, and 7 as students represent and solve addition and subtraction problems, use mental strategies to add and subtract within 20, determine even and odd, and use addition to find the total number of objects in a rectangular array.
The common computation situation types teachers should focus on are in Table 1: Common Addition and Subtraction Situations in the Kansas Mathematics Standards. These situation types are result unknown, change unknown, and start unknown. Refer to “Chapter 9: Whole Number Computation” for more information on these situation types.
As students solve one- and two-step problems, expect them to use manipulatives such as base-ten blocks, a number line, hundreds charts, etc. In second grade, do not focus on traditional algorithms or rules, but instead on the meaning of the operations.
The Operations and Algebraic Thinking tasks in the Illustrative Mathematics website is a good resource for connecting number sense to algebraic thinking. Illustrative Mathematics Grade 2 Operations & Algebraic Thinking tasks
Third Grade
All of the third grade standards under the Domain of Operations and Algebraic Thinking were addressed in Chapters 5 and 7 as students represent and solve multiplication and division problems and understand the relationship between multiplication and division and understand the properties of multiplication. Furthermore, third grade students solve problems involving the four operations and identify and explain the arithmetic patterns.
The Operations and Algebraic Thinking tasks in the Illustrative Mathematics website is a good resource for connecting number sense to algebraic thinking. Illustrative Mathematics Grade 3 Operations & Algebraic Thinking tasks
Algebraic Thinking and Algebraic Concepts across the Elementary Grades
Kindergarten
In kindergarten, students identify, duplicate, and extend simple number patterns in preparation for creating rules that describe relationships (NCTM, 2006). Students in kindergarten see addition and subtraction equations as they decompose a set of objects into two sets. Students decompose numbers 1-10 at this level by using objects or drawings. They should record each decomposition by drawing a picture. If students write an equation, they must also share a pictorial representation or show using manipulatives. Additionally, students use the symbols +, -, and = in their decompositions.
Kindergarten students should have multiple opportunities to use Ten-Frames as they “make ten.” For example, consider the following three ways that students may solve this problem: A package has 10 pencils in it. There are 7 pencils in the package. How many pencils are missing?
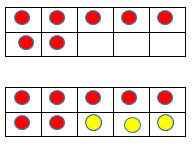
Kindergarten students solve problems fluently, which means efficiently, accurately, and flexibly. Accuracy means getting a correct answer, efficiently means solving a problem in a reasonable amount of steps, and flexibly means using strategies such as make ten, counting on, using doubles, using the commutative property, using fact families, etc. Fluency does not mean knowing the answer instantly. Read the paper, “Fluency is More than Speed” by clicking here.
First Grade
First grade students identify, describe, and apply number patterns and properties in order to develop strategies for basic facts (NCTM, 2006). Students in first grade solve addition and subtraction word problems with 20. At this level, do not use letters for the unknown symbols; instead use a box, picture, or a question mark.
Example: 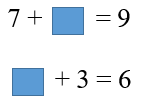
In first grade, students are learning to mathematize as they model addition and subtraction with objects, fingers, and drawings. This is foundational to algebraic thinking and problem solving. It is critical that students understand the problem situation and represent the problem.
Check out Greg Tang’s Word Problem Generator here. You can select the operation, the problem type, the unknown variable, and how many problems to generate.
As students solve word problems, it is critical that they not rely on keywords. When students use keywords when solving a problem, they will strip the numbers from the problem and do not consider the context of the problem. In addition, many “keywords” have multiple meanings, such as altogether and left. The use of a keyword strategy does not develop sense-making and does not build structures for more advanced learning. Instead, discuss what the problem is asking and move the question to the beginning of the problem. Act out the problem, and write the corresponding equation.
Second Grade
In second grade, students use number patterns to extend their knowledge of properties (NCTM, 2006). They represent and solve addition and subtraction problems within 100. Continue to expect students to use base-ten blocks, hundreds charts, number lines, drawings, or equations to support their understanding.
Students in second grade are becoming fluent (efficient, accurate, and flexible) as they mentally add and subtract within 20. Give students multiple opportunities to write equations with two equal addends, such as 2 + 2 = 4 or 3 + 3 = 6. This lays the foundation for multiplication.
Third Grade
Third grade students understand the properties of multiplication and see the relationship between multiplication and division (NCTM, 2006). This is a fundamental step in developing algebraic readiness. Students focus on two models of division: partition and measurement.
In second grade, students used rectangular arrays to find the total number of objects, and wrote equations to represent the sum, such as a 5 x 5 array could be written as 5 + 5 + 5 + 5 + 5 = 25. See the modules at EngageNY for resources teaching algebraic thinking for third grade students. Students use the properties of multiplication (commutative, associate, and distributive properties) as they multiply and divide, and understand part/part/whole relationships as they make the connections between multiplication and division. To develop algebraic thinking and reasoning, students explain an arithmetic pattern using the properties of operations.

Algebraic thinking is a Domain throughout the mathematics standards. Beginning in kindergarten, students solve addition and subtraction problems by representing them in various ways. Additionally, they learn about basic operations and quantitative relationships as they model problems and look at mathematical properties and relationships (Stramel, 2021). Read more about Operations and Algebraic Thinking in the K-5 Learning Progressions document.
a relational symbol used to indicate equality
a pattern that changes by the same rate, such as adding or subtracting the same value each time
the process of seeing and focusing on the mathematical aspects and ignoring the non mathematical aspects
a problem where you know the total number of groups, and are trying to find the number of items in each group
also called repeated subtraction division, a way of understanding division in which you divide an amount into groups of a given size

