As a teacher of mathematics, remember these fundamental beliefs as you develop early number concepts in your students.

1. Thinking about the problem, not just the answer, is what is most important.
2. The teacher should be the facilitator, not the one with all the answers.
3. Process is more important than product. Mathematics is not just “facts” to be memorized. The concepts children learn are of utmost importance; and then the memorization will come. Children must experience through play and using manipulatives and “reinvent” the concepts of mathematics in their own minds.

To help children develop early early number concepts, use activities that focus on verbal counting, one-to-one correspondence, cardinality, and subitizing.

Watch this video from Graham Fletcher on “The Progression of Early Number & Counting.”

Verbal counting is critical in developing quantitative thinking in young children. A focus on counting in context is one way to build a child’s mathematical abilities, therefore it is critical to count with children every day. Some activities include:

• Practice counting words and written numerals with pictures or representations of objects.
• Count aloud as a class.
• Use a number chart so children can see what number symbols look like visually.

For more activities related to counting, go to the K-5 Counting Center.

Suggested Activity:

To practice counting on, begin with a number and context the child recognizes, like four bear manipulatives. Add another bear and say, “five,” then add another bear and say, “six.” This helps students connect the number names with the increase in objects.

Help students see the patterns and make connections. Ask probing questions such as, “How do you know?” and “How did you figure that out?”

One-to-one correspondence is a developmental skill for young children that we take for granted. When a child touches each toy and says the number name out loud, “one, two, three…,” he/she demonstrates the ability to count with one-to-one correspondence. To develop this skill in young children, you can point to objects as you say the number word, or move each object as you say the number word out loud.

Suggested Activity:

To develop one-to-one correspondence, ask students to match two different types of objects together, such as counting bears and a die that shows five dots.

To be successful in mathematics, students must understand cardinality by counting various objects and hold that number “in their head.” A child who understands the cardinality concept will count a set once and not need to count it again.

To develop this skill, students need constant repetition of counting and teaching through modeling. Children learn how to count (matching counting words with objects) before they understand that the last word stated in a count indicates the amount of the set. Counting should be reinforced throughout the day, not just during “math time.”

Suggested Activity:

Show students a collection of counters. Ask, “How many are here?”

Other examples:

• Ask students to count the number of empty chairs in the classroom.
• Count the number of groups.
• Count the number of crayons in their desk.

Next in the progression of counting is subitizing, the ability to quickly identify the number of items in a group without counting the items. Developing the ability to subitize is critical to the success of early number concepts. Subitizing allows children to see groupings, and these groupings are foundational to addition, subtraction, multiplication and division.

Christina Tondevold (2019) explains: “It’s the same thing when kids are learning to read. When we first teach kids to learn to read, they do it in isolation. C-A-T. And then they put that together to make cat. It’s the same thing as 1, 2, 3, that’s 3. But eventually, we don’t want them saying “C-A-T,” and having to sound it all out the whole way. Like for catnap, you don’t want them to sound out “c-a-t-n-a-p.” You want them to see the chunks. Cat-nap.”

In mathematics, when adding 8 + 7, students may not immediately know the sum. But instead of counting on fingers, students can visualize these amounts. Students may see the 7 as 5 and 2 and the 8 as 5 and 3. They can then put together the 5 and 5 and the 2 and 3 to know 10 and 5 is 15.

Games are an excellent way to develop subitizing skills in young students; dice, dominoes, playing cards, etc. Watch the subitizing video, as groups of objects quickly flash on the screen.

Suggested Activity: Subitizing with Paper Plates

Hold up a paper plate with dots on it for 3 seconds and say, “How many dots did you see? What does the pattern look like?” Spend time discussing the configuration of the pattern and how many dots are on the plate. Then show the plate again so children can self-check. (Van de Walle, Karp, Bay-Williams, 2019)

The goal is for the children to recognize the shape of the dots on the plate and when held up, they will recognize that it’s a five or a 9 relatively quickly. You want the children to get past one to one counting of the dots and to recognize the number by the dot arrangement. Think of how you recognize the number on dice, you don’t count the pips but you know when you see a 5. This is what you want your children to learn.

Number Sense

Number sense is defined as a “good intuition about numbers and their relations. It develops gradually as a result of exploring numbers, visualizing them in a variety of contexts, and relating them in ways that are not limited by traditional algorithms” (Howden, 1989). When students consider the context of a problem, look at the numbers in a problem, and make a decision about which strategy would be most efficient in each particular problem, they have number sense. Number sense is the ability to think flexibly between a variety of strategies in context.

Building on subitizing, composing and decomposing numbers, using ten-frames, and the hundreds chart will help develop number sense in your students. When students have number sense, they gain computational fluency, are flexible in their thinking, and are able to choose the most efficient strategy to solve a problem.

Number sense is a foundational idea in mathematics; it encourages students to think flexibly and promotes confidence with numbers. According to Marilyn Burns (2007), “students come to understand that numbers are meaningful and outcomes are sensible and expected.” And “just as our understanding of phonemic awareness has revolutionized the teaching of beginning reading, the influence of number sense on early math development and more complex mathematical thinking carries implications for instruction” (Gersten & Chard, 1999).

Number sense is a skill that allows students to work with numbers fluently and efficiently. This includes understanding skills such as quantities, concepts of more and less, symbols represent quantities (8 means the same thing as eight), and making number comparisons (12 is greater than 9, and three is half of six). Students must

1. Understand numbers, ways of representing numbers, relationships among numbers, and the number system,
2. Understand the meanings of operations and how they related to one another, and
3. Compute fluently and make reasonable estimates (NCTM, 2000).

Teachers must give students many opportunities to develop number sense through activities with physical objects, such as counters, blocks, or small toys. Most children need that concrete experience of physically manipulating groups of objects. After these essential experiences, a teacher can move to more abstract materials such as dot cards.

Ten-Frames

Another way to develop number sense in children is to use ten-frames. A “ten-frame” is a rectangle, separated into two rows, with 10 equal spaces. Here is a blank ten-frame from NRICH.

Ten-frames help students develop number sense, a sense of ten, and learn basic number facts. A ten-frame also gives students a visual of numbers, of composing and decomposing numbers, and is a good way to teach addition and subtraction within 10.

This Ten Frame applet from NCTM Illuminations is a fun way for students to practice counting and addition skills.

Hundreds Chart

A Hundreds Chart is essential in every K-2 classroom. Ask students what patterns they see on the Hundreds Chart. You can also begin to “hide” numbers on the Hundreds Chart and ask students to tell what that number is and how they know.

Part-Part-Whole Relationships

Teaching part-part-whole relationships is critical to understanding addition and subtraction concepts. The part-part-whole model shows that two parts make up a whole. The following examples show the value of part-part-whole relationships.

Example #1: Samantha has 4 red marbles and 3 blue stickers. How many stickers does Samantha have?

To use the part-part-whole model, think first about the unknown. Since we want to know how many stickers Samantha has in all, that is the unknown or the “whole.”

Example #2: Addison has 27 chocolate candies. 15 are red, and the rest are green. How many green candies does Addison have?

To use the part-part-whole model, think first about the unknown. Since we want to know how many of Addison’s candies are green, that is the unknown or the “part.”

Basic facts are any number or mathematical fact or idea that is instantly recognizable or retrievable without having to resort to a strategy or a calculation. Just knowing basic facts is not enough. Teachers must help students develop the ability to quickly and accurately understand the relationships between numbers. Students need to make sense of numbers as they find and make strategies for joining and separating quantities.

Students use properties of addition (the commutative and associative properties) to add whole numbers. They can then use other strategies such as making tens and near doubles. (Student do not need to know the names of the properties, but they should understand them.)

In the strategy “making tens,” students decompose numbers to find a 10. For example, when learning 8 + 5, students may decompose the 5 into 2 and 3, and then see that 8 + 2 is 10; therefore 10 + 3 = 13.

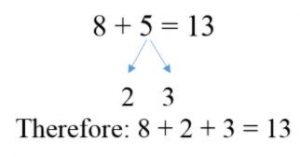
Giving children multiple opportunities to experience early number concepts and number sense is critical for early childhood teachers. Children must experience mathematics through play and manipulatives as they make sense of numbers in their own minds.