9 Early Fraction Concepts

What are Fractions?

According to the Kansas Mathematics Standards (2017), the formal definition of fraction is a number expressible in the form [latex]\frac{a}{b}[/latex] where a is the number of equal parts being referenced and b is the number of equal parts in the whole. But what does this mean?

The word “fraction” comes from the Latin word fractus or broken. A fraction describes how many parts of a certain size there are, for example, one-half, three-fourths, etc. Additionally, the top number (numerator) says how many parts you have, and the bottom number (denominator) says how many equal parts in the whole amount. Most importantly, a fraction is a number.

An understanding of fractions begins in first grade when students partition circles and rectangles into two and four equal parts, and describe the parts with the words halves, fourths, and quarters. In second grade, students partition circles and rectangles in two, three, and four equal parts, and describe those parts with the words halves, thirds, and fourths. Fractions become the major emphasis in third grade as students look at fraction symbols, and explore unit fractions.

“Students need significant time and experiences to develop a deep conceptual understanding” of fractions (Van de Walle, Karp, Bay-Williams, 2019, p. 338). Teachers typically begin fraction instruction with objects, paper folding, or even plastic fraction circles. But often we move too quickly past these models to abstract computation. Some experts even argue that drawings of fractions fail to be concrete enough for some students. The act of cutting and folding and manipulating is critical for all students.

Watch this video from Graham Fletcher, “The Progression of Fractions.”

Fraction Constructs

Fractions include many meanings such as part-whole, measurement, division, operator, and ratio. Understanding fractions includes the need to understand all of these different meanings. As you and your students begin to make sense of fractions, you must also understand all the possible concepts that fractions represent. The following constructs are based on the research from Van de Walle, Karp, and Bay-Williams (2019):

Fractions as Part-whole Comparisons. Part-whole comparisons is a good place to start when building a conceptual understanding of fractions. Part-whole comparisons can be shown by shading a region, part of a group, and measurement.

• Shading a region 

For example, a circle can be divided into four equal parts. If three of those parts are shaded pink, then the fraction shaded is [latex]\frac{3}{4}[/latex].

• Part of a group

For example, I have five pets; three cats and two dogs. The fractional part of cats to all of my pets is [latex]\frac{3}{5}[/latex].

• Measurement

For example, in the fraction [latex]\frac{3}{8}[/latex], students use the unit fraction[latex]\frac{1}{8}[/latex]to count or measure that it takes 3 of those units to reach [latex]\frac{3}{8}[/latex].

Fractions as Division. Just like with whole numbers, division means making equal-sized groups. Students understand the connection to equal- and fair-sharing which builds from their experiences with sharing and partitioning. For example, “Eight friends are sharing four apples. How much of an apple will each person receive?” Each person will get [latex]\frac{4}{8}[/latex] or [latex]\frac{1}{2}[/latex]of an apple.

A fraction is the quotient of division of two integers. For example, if you want to divide three things equally among 5 people, students know to this can be solved with division, although the quotient of [latex]\frac{3}{5}[/latex] cannot be represented with a whole number, so new numbers need to be introduced; the fraction [latex]\frac{3}{5}[/latex].

Fractions as Operators. This construct builds on the concepts of seeing a fraction as a multiple of a unit fraction. To find [latex]\frac{3}{4}[/latex] of something, you could divide by 4 and then multiply by 3, or multiply by 3 and then divide by 4. The result would be a smaller quantity than the original. For example, [latex]\frac{3}{4}[/latex] x 12 = 9.

Fractions as Ratios. Ratio is another meaning of fractions. For example, [latex]\frac{5}{8}[/latex] can be seen as the probability of an event being five in eight. Ratios can be expressed in two different ways: part-part, such as the ratio of boys to girls in class, and part-whole, such as the ratio of boys to the whole class.

The Language of Fractions

The language of fractions is critical to students developing a conceptual understanding of fractions. But this does not mean that teachers teach only the definitions of fractions, but instead teachers should first focus on making sense of what fractions are. Fractions are a way to describe and represent a part of a whole.

Students first begin to make sense of fractions in first grade when they compose and decompose plane figures, such as putting together two triangles to make a quadrilateral. First grade students must have multiple opportunities and many experiences with the words halves, fourths, and quarters. According to Van de Walle, Karp, and Bay-Williams (2019), the best time to introduce these words to students is during problem solving, not before. For example, when students are cutting a pan of brownies into four equal shares, the teacher can say, “We call these fourths. The whole is cut into four equal-size parts called fourths.”

In second grade, students add to their fraction vocabulary the word “third,” but students are not introduced to the traditional fractional notation until third grade when they develop an understanding of unit fractions. Additionally, the fraction expectations in third grade are limited to fractions with denominators of 2, 3, 4, 6, and 8. It is in third grade that students develop an understanding of fractions as numbers, use the fraction symbols, and use area and linear models. Third grade lays the foundation for an understanding of fractions and is critical for students to be successful in future mathematics.

The numerator is the “counting number,” or the number of parts we have.

The denominator is how many parts are in the whole.

When talking about these terms, be sure to ask students the following questions:

• “What does the numerator in the fraction tell us?”
• “What does the denominator in the fraction tell us?”
• “What would a fraction equal to one look like?”
• “How do you know if a fraction is less than or greater than one?”

Area – Fractions are determined on how much of a part or area relates to the whole area.

Length – Fractions can be represented on a number line, or as a distance between 0 and another point on the number line.

Set -Fractions can be represented based on how many items are in part of the whole set.

Fractions are Numbers

The most important thing young children need to understand is that fractions are numbers; they represent quantities that have values (Van de Walle, Karp, & Bay-Williams, 2019). Partitioning and iterating are two important actions that emphasize the numerical nature of fractions.

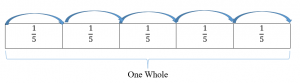
Partitioning is when students section or segment a shape into equal-sized parts. When partitioning, start with a unit fraction such as [latex]\frac{1}{3}[/latex]. One-third ([latex]\frac{1}{3}[/latex]) is the size of piece you would get by taking a whole and dividing it into 3 equal parts.

When students draw and see diagrams such as the one above, it emphasizes that fractions are a fraction of something. You would teach this by saying, “We call these pieces thirds because we cut the whole into three parts. All of these parts are the same size – thirds.”

Students are introduced to fractions in first grade as they are presented with the names for fractional parts – halves and fourths; in second grade, students partition circles and rectangles into two, three, and four equal parts, and describe those parts using the words halves, thirds, and fourths; fractional symbols are not introduced until third grade.

Iterating is when students perform the action of aligning, copying, or combining equal units to verify a fraction. According to Siebert (2007), “To conceive of a fraction from an iteration perspective, first start with a unit fraction, such as [latex]\frac{1}{5}[/latex]. How can you tell if something is [latex]\frac{1}{5}[/latex]? An amount is [latex]\frac{1}{5}[/latex] if five copies of it equals 1. The image here is of taking [latex]\frac{1}{5}[/latex] and iterating is 5 more times to make a whole.”

Equivalent Fractions and Fraction Comparisons

Equivalence is a core concept in mathematics. Equivalent fractions have the same value, even though they may look different. For example 12 and 24 are equivalent because they are both “half.”

Teachers must devote enough time so that their students have a deep understanding of this concept. Equivalent fractions and comparing fractions is first addressed in third grade, and then applied in fourth grade. The focus of both the third and fourth grade is to use visual fraction models so that students can explore the idea of equivalent fractions instead of using algorithms.

An important concept when comparing fractions is both the size of the parts and the number of parts. For example, [latex]\frac{1}{4}[/latex] is lesson than [latex]\frac{1}{2}[/latex] because when the whole is cut into 4 pieces, the pieces are smaller than when the whole is cut into 2 pieces. Students need to see this.

Students are not expected to generate a rule for equivalent fractions until fourth grade, although third grade students should notice the connections between the models and the fractions.

Fraction Equivalence

When teaching fraction equivalence, do not move to the traditional algorithm too quickly. Allow your students to make sense of the relationship between the two fractions first. After students have a conceptual understanding using visual representations and models, then you can ask if they see patterns in the way the fractional parts are counted (Stramel, 2021).